题目内容
已知圆C: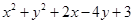 =0
=0
(1)已知不过原点的直线 与圆C相切,且在
与圆C相切,且在 轴,
轴,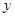 轴上的截距相等,求直线
轴上的截距相等,求直线 的方程;
的方程;
(2)求经过原点且被圆C截得的线段长为2的直线方程
(1)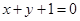 或
或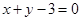 ;(2)
;(2) ,
,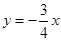
解析试题分析:(1)因为已知不过原点的直线 与圆C相切,且在
与圆C相切,且在 轴,
轴,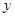 轴上的截距相等,所以可以假设所求的直线为
轴上的截距相等,所以可以假设所求的直线为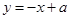 ,又因为该直线与圆相切所以圆C:
,又因为该直线与圆相切所以圆C: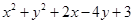 =0的圆心(-1,2)到直线的距离等于圆的半径
=0的圆心(-1,2)到直线的距离等于圆的半径 即可求出
即可求出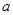 的值
的值
(2)求经过原点且被圆C截得的线段长为2的直线方程,要分两类i)直线的斜率不存在;ii)直线的斜率存在 再根据点到直线的距离即可求得结论
试题解析:(1)∵切线在两坐标轴上截距相等且不为零,设直线方程为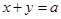 1分
1分
∴圆心C(-1,2)到切线的距离等于圆半径 , 3分
, 3分
即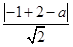 =
= 4分
4分
∴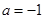 或
或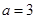 5分
5分
所求切线方程为: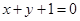 或
或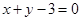 6分
6分
(2)当直线斜率不存在时,直线即为y轴,此时,交点坐标为(0,1),(0,3),线段长为2,符合故直线 8分
8分
当直线斜率存在时,设直线方程为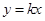 ,即
,即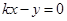
由已知得,圆心到直线的距离为1, 9分
则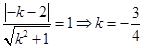 , 11分
, 11分
直线方程为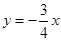
综上,直线方程为 ,
,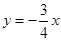 12分
12分
考点:1 点到直线的距离 2 直线与圆的位置关系 3 直线方程的表示

练习册系列答案
相关题目
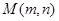 为圆C上任意一点,求
为圆C上任意一点,求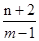 的最大值与最小值;
的最大值与最小值;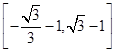 ,求直线AB的倾斜角α的取值范围.
,求直线AB的倾斜角α的取值范围.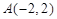 并且和
并且和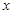 轴的正半轴、
轴的正半轴、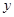 轴的正半轴所围成的三角形的面积是
轴的正半轴所围成的三角形的面积是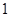 的直线方程.
的直线方程.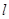 :
: 和
和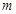 :
: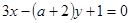 互相平行,求实数
互相平行,求实数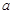 的值.
的值.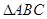 的顶点
的顶点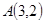 ,
,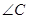 的平分线
的平分线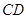 所在直线方程为
所在直线方程为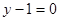 ,
,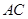 边上的高
边上的高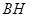 所在直线方程为
所在直线方程为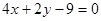 .
.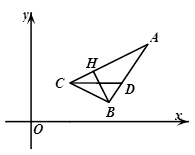
 的坐标;
的坐标;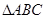 的面积.
的面积.  的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程: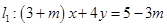 ,
,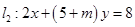 ;
; 为何值时,
为何值时,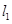 与
与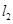 (1)相交;(2)平行;(3)垂直.
(1)相交;(2)平行;(3)垂直.