题目内容
【题目】已知直线l:y=﹣x+1与椭圆C: ![]() =1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为(
=1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为( ![]() ,
, ![]() )
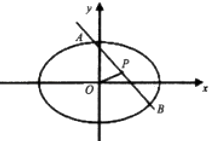
) 
(1)求椭圆C离心率;
(2)设O为坐标原点,且2|OP|=|AB|,求椭圆C的方程.
【答案】
(1)解:将直线y=1﹣x代入椭圆方程,可得
(b2+a2)x2﹣2a2x+a2﹣a2b2=0,
则x1+x2= ![]() ,
,
由AB的中点P的坐标为( ![]() ,
, ![]() ),可得
),可得
![]() =
= ![]() ,即为a2=2b2,
,即为a2=2b2,
可得c2=a2﹣b2= ![]() a2,
a2,
则椭圆C离心率为e= ![]() =
= ![]()
(2)解:由(1)可得,
△=4a4﹣4(b2+a2)(a2﹣a2b2)>0,
可得a2+b2>1,即b2> ![]() ,
,
x1+x2= ![]() ,x1x2=
,x1x2= ![]() =
= ![]() ,
,
由2|OP|=|AB|,可得:
2 ![]() =
= ![]()
![]() ,
,
解得b2= ![]() (满足△>0),即有a2=
(满足△>0),即有a2= ![]() ,
,
可得椭圆方程为 ![]() =1
=1
【解析】(1)将直线方程代入椭圆方程,运用韦达定理和中点坐标公式,结合离心率公式计算即可得到所求值;(2)运用韦达定理和弦长公式,以及两点的距离公式,解方程即可得到a,b,进而得到椭圆方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

