题目内容
3．若定义在R上的偶函数f（x）在区间（-∞，0]上单调递减，且f（2）=0，求使得f（x）＜0的x的范围．分析 根据函数奇偶性和单调性之间的关系，将不等式进行转化即可得到结论．
解答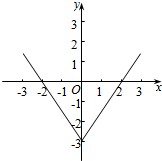 
解：∵函数f（x）是定义在R上的偶函数，在（-∞，0]上是减函数，
∴函数f（x）在[0，+∞）上为增函数，且f（-2）=-f（2）=0，
作出函数f（x）的草图：
如图：则不等式等价为f（x）＜0的解为-2＜x＜2，
故不等式的解集为（-2，2）．
点评 本题主要考查不等式的解集，利用函数奇偶性和单调性之间的关系是解决本题的关键．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
8．如果loga2＞logb2＞0，那么（ ）
| A． | 1＜a＜b | B． | 1＜b＜a | C． | 0＜a＜b＜1 | D． | 0＜b＜a＜1 |
12．已知|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=5，$\overrightarrow{a}$与$\overrightarrow{b}$不共线，若向量k$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$互相垂直，则实数k的值为（ ）
| A． | $\frac{5}{3}$ | B． | $\frac{3}{5}$ | C． | ±$\frac{3}{5}$ | D． | ±$\frac{5}{3}$ |