��Ŀ����
����Ŀ����ͼ1���߶�![]() �ij���Ϊ
�ij���Ϊ![]() �����߶�
�����߶�![]() ��ȡ������
��ȡ������![]() ��ʹ��
��ʹ��![]() ����
����![]() Ϊһ�����߶�
Ϊһ�����߶�![]() ���Ϸ���һ���������Σ�Ȼ��ȥ���߶�
���Ϸ���һ���������Σ�Ȼ��ȥ���߶�![]() ���õ�ͼ2�е�ͼ������ͼ2�е����Ϸ����߶�
���õ�ͼ2�е�ͼ������ͼ2�е����Ϸ����߶�![]() ����ͬ�IJ������õ�ͼ3�е�ͼ�����������ƣ����Ǿ͵õ�������һϵ��ͼ�Σ�
����ͬ�IJ������õ�ͼ3�е�ͼ�����������ƣ����Ǿ͵õ�������һϵ��ͼ�Σ�

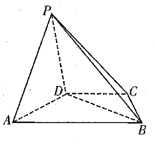
�ǵ�![]() ��ͼ�Σ�ͼ1Ϊ��1��ͼ�����е������߶γ��ĺ�Ϊ
��ͼ�Σ�ͼ1Ϊ��1��ͼ�����е������߶γ��ĺ�Ϊ![]() ���ָ����й�����
���ָ����й�����![]() ���ĸ����⣺
���ĸ����⣺
������![]() �ǵȱ����У�
�ǵȱ����У�
������![]() �ǵ������У�
�ǵ������У�
�۴�����С������![]() ��ʹ�ö������������
��ʹ�ö������������![]() ������
������![]() ��
��
�ܴ�����������![]() ��ʹ�ö������������
��ʹ�ö������������![]() ������
������![]() .
.
����������������__________�� (�������������������.
���𰸡��ڢ�
���������������������![]() �ǵ�ǰ����ɵõ��ٴ����ڶԣ����õȱ��������ʽ���
�ǵ�ǰ����ɵõ��ٴ����ڶԣ����õȱ��������ʽ���![]() �����ò���ʽ��������жϢ۴����ܶ�.
�����ò���ʽ��������жϢ۴����ܶ�.
��⣺��ͼ��֪��![]()
![]() ��
��
![]() ���ǵȱ����У��ٴ���
���ǵȱ����У��ٴ���
![]() �ǵ������У�����ȷ��
�ǵ������У�����ȷ��
![]()
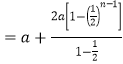
![]() ��
��
���ڢۣ�![]() ��Ҫʹ
��Ҫʹ![]() �������
�������
ֻ��![]() ��
��![]() ����Сֵ���۴���
����Сֵ���۴���
���ڢܣ�![]() ��Ҫʹ
��Ҫʹ![]() �������
�������
ֻ��![]() ����
����![]() �����ֵΪ
�����ֵΪ![]() ������ȷ��
������ȷ��
�������Ǣڢܣ��ʴ�Ϊ�ڢ�.

 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�����Ŀ����һλͬѧ���↑��һ��С����,��Ϊ���о����¶��Ȳ����۵�Ӱ��,����ͳ��,�õ�һ�������Ȳ豭���뵱�����µĶԱȱ�����:
����x/�� | -5 | 0 | 4 | 7 | 12 | 15 | 19 | 23 | 27 | 31 | 36 |
�Ȳ����۱���y/�� | 156 | 150 | 132 | 128 | 130 | 116 | 104 | 89 | 93 | 76 | 54 |
(1)����ɢ��ͼ;
(2)���ܴ�ɢ��ͼ�з����������Ȳ�����۱���֮���ϵ��һ�������?
(3)������Ƴ����Թ�ϵ�Ļ�,�뻭��һ��ֱ�������Ƶر�ʾ�������Թ�ϵ;
(4)������ع�ֱ�߷���;
(5)����(4)�Ļع鷽��,��ij���������2 ��,Ԥ����һ�������Ȳ�ı���.
����Ŀ��ij����Ϊ�˽�˿͵Ĺ�����������ʱ�����Ϣ������һ��Ա������ռ����ڸó��й����100λ�˿͵�������ݣ����±���ʾ��
һ���Թ����� | 1��4�� | 5 ��8�� | 9��12�� | 13��16�� | 17�������� |
�˿������ˣ� | x | 30 | 25 | y | 10 |
����ʱ�䣨����/�ˣ� | 1 | 1.5 | 2 | 2.5 | 3 |
��֪��100λ�˿��е�һ�ι���������8���Ĺ˿�ռ55%��
��1��ȷ��x��y��ֵ������˿�һ�ι���Ľ���ʱ��X�ķֲ�������ѧ������
��2����ij�˿͵�������̨ʱǰ��ǡ��2λ�˿�����㣬�Ҹ��˿͵Ľ������������ù˿ͽ���ǰ�ĵȺ�ʱ�䲻����2.5���ӵĸ��ʣ���ע����Ƶ����Ϊ���ʣ�