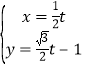题目内容
【题目】已知奇函数![]() .
.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在其定义域上的单调性,并用定义证明;
在其定义域上的单调性,并用定义证明;
(3)若![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)函数
(2)函数![]() 是R上的增函数,证明见解析(3)
是R上的增函数,证明见解析(3)![]()
【解析】
(1)根据奇函数性质,可知![]() ,代入即可求得
,代入即可求得![]() 的值.
的值.
(2)利用定义,![]() ,作差
,作差![]() 后,将整式变形后即可判断符号,进而判断函数
后,将整式变形后即可判断符号,进而判断函数![]() 的单调性.
的单调性.
(3)根据奇函数的性质,结合单调递增,即可将不等式变形为![]() ;结合辅助角公式及恒成立问题,解关于m的不等式组即可求得
;结合辅助角公式及恒成立问题,解关于m的不等式组即可求得![]() 的取值范围.
的取值范围.
(1)若![]() 为奇函数,
为奇函数,
则![]() ,
,
解得![]() .
.
(2)由(1)可知,![]() .则
.则![]() 是R上的增函数.
是R上的增函数.
证明:任取![]() ,
,
则![]()
![]()
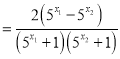
![]()
![]() 且
且![]()
![]()
即![]()
所以函数![]() 是R上的增函数.
是R上的增函数.
(3)若![]() 对所有的
对所有的![]() 恒成立,
恒成立,
因为![]() 是奇函数,
是奇函数,
![]() 对所有的
对所有的![]() 恒成立.
恒成立.
因为![]() 是R上的增函数,
是R上的增函数,
![]() 对所有的
对所有的![]() 恒成立.
恒成立.
即![]() 对所有的
对所有的![]() 恒成立.
恒成立.
利用辅助角公式变形可得![]()
因为对所有的![]() 恒成立.
恒成立.
![]() .
.
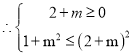 ,
,
解得![]() .
.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目