题目内容
11.已知y=a-bcos2x(b>0)的最大值是$\frac{3}{2}$,最小值是-$\frac{1}{2}$,求函数y=-4asin(3bx+$\frac{π}{3}$)的周期、最大值及取得最大值时x的值的集合.分析 根据三角函数的性质先求出a,b的值,即可得到结论.
解答 解:∵b>0,y=a-bcos2x(b>0)的最大值是$\frac{3}{2}$,最小值是-$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{a-b=-\frac{1}{2}}\\{a+b=\frac{3}{2}}\end{array}\right.$,得a=$\frac{1}{2}$,b=1,
则函数y=-4asin(3bx+$\frac{π}{3}$)=-2sin(3x+$\frac{π}{3}$),
则函数的周期T=$\frac{2π}{3}$,
当sin(3x+$\frac{π}{3}$)=-1,即3x+$\frac{π}{3}$=-$\frac{π}{2}$+2kπ,
即x=-$\frac{5π}{18}$+$\frac{2kπ}{3}$,k∈Z时,函数y=-2sin(3x+$\frac{π}{3}$)取得最大值2,
此时x的集合为{x|x=-$\frac{5π}{18}$+$\frac{2kπ}{3}$,k∈Z}.
点评 本题主要考查三角函数的周期性,最值的性质,根据条件求出a,b的值是解决本题的关键.

练习册系列答案
相关题目
1.先将函数y=sin2x的图象向右平移$\frac{π}{3}$个单位长度,再作所得的图象关于y轴的对称图形,则最后函数图象的解析式为( )
| A. | $y=sin(-2x-\frac{2π}{3})$ | B. | $y=sin(-2x+\frac{2π}{3})$ | C. | $y=sin(-2x-\frac{π}{3})$ | D. | $y=sin(-2x+\frac{π}{3})$ |
16.如图所示的程序框图的运行结果是( )
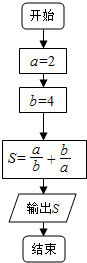

| A. | 2 | B. | 2.5 | C. | 3.5 | D. | 4 |
20.下列说法正确的是( )
| A. | 对于相关系数r来说,|r|≤1,|r|越接近0,相关程度越大;|r|越接近1,相关程度越小 | |
| B. | 对于相关系数r来说,|r|≥1,|r|越接近1,相关程度越大;|r|越大,相关程度越小 | |
| C. | 对于相关系数r来说,|r|≤1,|r|越接近1,相关程度越大;|r|越接近0,相关程度越小 | |
| D. | 对于相关系数r来说,|r|≥1,|r|越接近1,相关程度越小;|r|越大,相关程度越大 |
1.平行四边形ABCD中,AD=1,∠BAD=60°,E为CD中点.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=1,则|AB|=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |