题目内容
2.设a≠0,函数f(x)=ax3-3x2.(1)若函数y=f(x)在[0,1]的最小值为-2,求a的值;
(2)若函数g(x)=exf(x)在[0,2]上是单调减函数,求实数a的取值范围.
分析 (Ⅰ)先求出函数f(x)的导数,通过讨论a的范围,得到函数的单调性,从而求出函数的最小值,进而求出a的值;
(Ⅱ)由在[0,2]上是单调减函数可转化成在[0,2]上导函数恒小于零,再借助参数分离法分离出参数a,再利用导数法求出另一侧的最值即可
解答 解:(Ⅰ)∵f(x)=ax3-3x2,a≠0,
∴f′(x)=3ax2-3x=3x(ax-1),
∴当a>0时,
由f′(x)>0得:x>$\frac{1}{a}$
由f′(x)<0得:x<$\frac{1}{a}$,
∴当a>0时,函数f(x)的单调递增区间为(-∞,$\frac{1}{a}$),递增区间是($\frac{1}{a}$,+∞);
当$\frac{1}{a}$≥1,即:0<a≤1时,f(x)在[0,1]递减,f(x)最小值=f(1)=a-3=-2,解得:a=1,符合题意;
当0<$\frac{1}{a}$<1,即a>1时,f(x)在[0,$\frac{1}{a}$)递减,在($\frac{1}{a}$,1]递增,
∴f(x)最小值=f($\frac{1}{a}$)=-2,解得:a=-1或a=1(舍),
当a<0时,由f′(x)>0得:x∈∅,由f′(x)<0得:x∈R;
函数f(x)的单调递减区间为R;
∴f(x)最小值=f(1)=a-3=-2,解得:a=1,不合题意;
综上:a=1.
(Ⅱ)由题设,g′(x)=ex(ax3-3x2+3ax2-6x),又ex>0,
所以,?x∈(0,2],ax3-3x2+3ax2-6x≤0,
这等价于,不等式a≤$\frac{{3x}^{2}+6x}{{x}^{3}+{3x}^{2}}$=$\frac{3x+6}{{x}^{2}+3x}$对x∈(0,2]恒成立.
令h(x)=$\frac{3x+6}{{x}^{2}+3x}$(x∈(0,2]),
则h′(x)=-$\frac{3{(x}^{2}+4x+6)}{{{(x}^{2}+3x)}^{2}}$=-$\frac{3{[(x+2)}^{2}+2]}{{{(x}^{2}+3x)}^{2}}$<0,
所以h(x)在区间(0,2]上是减函数,
所以h(x)的最小值为h(2)=$\frac{6}{5}$.
所以a≤$\frac{6}{5}$.即实数a的取值范围为:{a|a≤$\frac{6}{5}$且a≠0}.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,函数恒成立问题,本题属于中档题.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | 有两个面平行,其余各面都是平行四边形的几何体是棱柱 | |
| B. | 用斜二测法画平行四边形的直观图一定是平行四边形 | |
| C. | 用一个面去截棱锥,底面和斜面之间的部分组成的几何体叫做棱台 | |
| D. | 平行与同一平面的两条直线平行 |
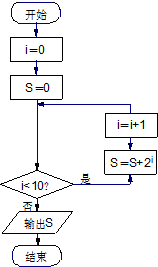
| A. | 1023 | B. | 1024 | C. | 511 | D. | 2047 |
| A. | ${(\frac{1}{4})^2}×(\frac{3}{4})$ | B. | ${(\frac{3}{4})^2}×(\frac{1}{4})$ | C. | $C_3^2{(\frac{1}{4})^2}×(\frac{3}{4})$ | D. | $C_3^2{(\frac{3}{4})^2}×(\frac{1}{4})$ |
