题目内容
已知向量a=(1,2),b=(2,3),则λ<-4是向量m=λa+b与向量n=(3,-1)夹角为钝角的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
m=(λ+2,2λ+3),m,n的夹角为钝角的充要条件是m·n<0且m≠μn(μ<0).m·n<0,即3(λ+2)-(2λ+3)<0,即λ<-3;若m=μn,则λ+2=
3μ,2λ+3=-μ,解得μ= ,故m≠μn(μ<0),所以,m,n的夹角为钝角的充要条件是λ<-3.λ<-4是m,n的夹角为钝角的充分而不必要条件.
,故m≠μn(μ<0),所以,m,n的夹角为钝角的充要条件是λ<-3.λ<-4是m,n的夹角为钝角的充分而不必要条件.
3μ,2λ+3=-μ,解得μ=
 ,故m≠μn(μ<0),所以,m,n的夹角为钝角的充要条件是λ<-3.λ<-4是m,n的夹角为钝角的充分而不必要条件.
,故m≠μn(μ<0),所以,m,n的夹角为钝角的充要条件是λ<-3.λ<-4是m,n的夹角为钝角的充分而不必要条件.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
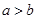 ”是“
”是“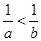 ”成立的( )
”成立的( )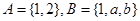 ,则“
,则“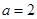 ”是“
”是“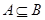 ”的( )
”的( ) 为真”是“
为真”是“ 为真”的充分不必要条件;
为真”的充分不必要条件; ,且
,且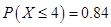 ,则
,则 ;
; ,则不等式
,则不等式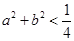 成立的概率是
成立的概率是 ;
; ,若
,若 ,
, ,则
,则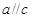 .
. 与
与 对应的斜率分别为
对应的斜率分别为 与
与 ,则“
,则“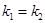 ”是“
”是“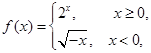 则
则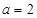 是
是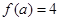 成立的 ( )
成立的 ( ) ;条件
;条件 ,那么
,那么 是
是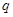 的( ) 条件
的( ) 条件