题目内容
 (2011•重庆三模)已知双曲线C:
(2011•重庆三模)已知双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| 3 |
| 2 |
(Ⅰ)求双曲线C的方程;
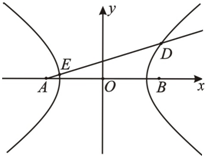
(Ⅱ)如题20图:设双曲线C的左右焦点分别为A,B,点D为该双曲线右支上一点,直线AD与其左支交于点E,若
| AE |
| ED |
分析:(I)由题意可得,
可求a,c,由b2=c2-a2可求b,可求双曲线的方程
(II)由(I)知A(-2,0),设D(x0,y0),E(x1,y1)则由
=λ
可得x1=
,y1=
,结合E,D在双曲线上,可求x0,结合双曲线的性质可求λ
|
(II)由(I)知A(-2,0),设D(x0,y0),E(x1,y1)则由
| AE |
| ED |
| λx0-2 |
| 1+λ |
| λy0 |
| 1+λ |
解答:解(I)由题意可得,
∴
∴双曲线的方程为
-y2=1(4分)
(II)由(I)知A(-2,0),设D(x0,y0),E(x1,y1)
∴
=(x1+2,y1),
=(x0-x1,y0-y1)
则由
=λ
可得x1=
,y1=
∵E在双曲线上
∴
-y12=1
∴(-2+λx0)2-3(λy0)2=3(1+λ)2
∵D在双曲线
∴3y02=x02-3
代入上式可得,x0=
∵x0≥
=a
∴
≥
∴λ≤
=
-
∵D在双曲线的左支,点D在右支
∴0<λ≤
-
(12分)
|
∴
|
∴双曲线的方程为
| x2 |
| 3 |
(II)由(I)知A(-2,0),设D(x0,y0),E(x1,y1)
∴
| AE |
| ED |
则由
| AE |
| ED |
可得x1=
| λx0-2 |
| 1+λ |
| λy0 |
| 1+λ |
∵E在双曲线上
∴
| x12 |
| 3 |
∴(-2+λx0)2-3(λy0)2=3(1+λ)2
∵D在双曲线
∴3y02=x02-3
代入上式可得,x0=
| 1-6λ |
| 4λ |
∵x0≥
| 3 |
∴
| 1-6λ |
| 4λ |
| 3 |
∴λ≤
| 1 | ||
6+4
|
| ||
| 3 |
| 1 |
| 2 |
∵D在双曲线的左支,点D在右支
∴0<λ≤
| ||
| 3 |
| 1 |
| 2 |
点评:本题主要考查了利用双曲线的性质求解双曲线的方程,双曲线的性质的应用,属于综合试题

练习册系列答案
相关题目