题目内容
设数列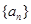 的前n项和为
的前n项和为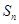 ,
,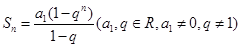
(1)求证:数列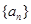 是等比数列;
是等比数列;
(2)若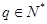 ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列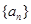 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。
(3)若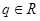 ,是否存在
,是否存在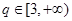 ,使数列
,使数列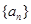 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。
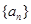 的前n项和为
的前n项和为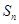 ,
,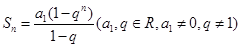
(1)求证:数列
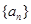 是等比数列;
是等比数列;(2)若
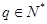 ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列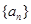 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由。(3)若
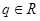 ,是否存在
,是否存在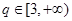 ,使数列
,使数列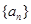 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由。解:(1)n=1时, ,
,
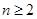 时,
时,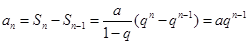 (n=1也符合)
(n=1也符合)
 ,
,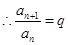 ,即数列
,即数列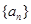 是等比数列。
是等比数列。
(2)若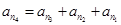 则
则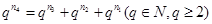
可设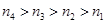 ,两边同除以
,两边同除以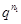 得:
得: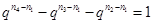
因为左边能被q整除,右边不能被q整除,因此满足条件的q不存在。
(3)若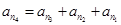 则
则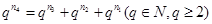
可设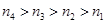 ,
,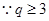 ,
,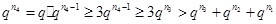 ,
,
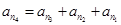 不成立。
不成立。
 ,
, 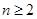 时,
时,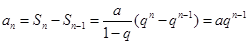 (n=1也符合)
(n=1也符合)  ,
,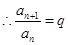 ,即数列
,即数列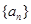 是等比数列。
是等比数列。 (2)若
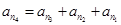 则
则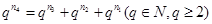
可设
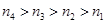 ,两边同除以
,两边同除以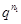 得:
得: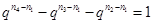
因为左边能被q整除,右边不能被q整除,因此满足条件的q不存在。
(3)若
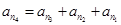 则
则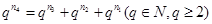
可设
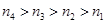 ,
,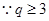 ,
,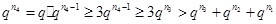 ,
,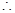
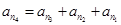 不成立。
不成立。略

练习册系列答案
相关题目
 、B
、B ;
;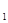 =200,求{A
=200,求{A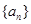 的前
的前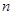 项和为
项和为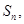 若
若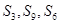 成等差数列,则( )
成等差数列,则( )



 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项和为
项和为 ,且
,且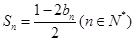
 ,求数列
,求数列 的前
的前
 }的前n项和为
}的前n项和为 。若
。若 ,则
,则 = .
= .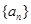 中:
中: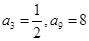 ,则
,则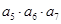 的值为
的值为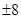
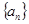 是等比数列,
是等比数列,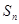 为其前n项和。
为其前n项和。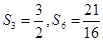 ,求
,求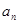 ;
;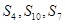 成等差数列,证明
成等差数列,证明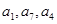 也成等差数列。
也成等差数列。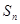 为等比数列
为等比数列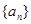 的前
的前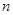 项的和,
项的和,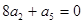 ,则
,则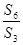 =___________
=___________