题目内容
(12分)在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在 一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:
一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:
(Ⅰ)甲、乙两单位的演出序号均为偶数的概率;
(Ⅱ)甲、乙两单位的演出序号不相邻的概率.
 一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:
一起. 若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……,6),求:(Ⅰ)甲、乙两单位的演出序号均为偶数的概率;
(Ⅱ)甲、乙两单位的演出序号不相邻的概率.
用(a,b)表示甲和乙的位置,有如下30 种等可能的基本事件。
种等可能的基本事件。
(1,2),(1,3)(1,4),(1,5),(1,6)
(2,1),(2,3)(2,4),(2,5), (2,6)
(2,6)
(3,1),(3,2)(3,4),(3,5),(3,6)
(4,1),(4,2)(4,3),(4,5),(4,6)
(5,1),(5,2)(5,3),(5,4),(5,6)
(6,1),(6,2)(6,3),(6,4),(6,5)
(Ⅰ)设A表示“甲、乙两单位的演出序号均为偶数”
则A包含如下6种基本事件:(2,4),(2,6),(4,2),(4,6),(6,2),(6,4)
据古典概型概率公式,故所求概率为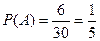
(Ⅱ)设B表示“甲、乙两单位的演出序号不相邻”
则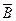 表示“甲、乙两单位的演出序号相邻”
表示“甲、乙两单位的演出序号相邻” 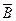 包含如
包含如 下10种基本事件:
下10种基本事件:
(1,2),(2,3),(3,4),(4,5),(5,6)
(2,1),(3,2),(4,3),(5,4),(6,5),
据古典概型概率公式,从而所求概率为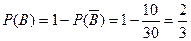
 种等可能的基本事件。
种等可能的基本事件。(1,2),(1,3)(1,4),(1,5),(1,6)
(2,1),(2,3)(2,4),(2,5),
 (2,6)
(2,6)(3,1),(3,2)(3,4),(3,5),(3,6)
(4,1),(4,2)(4,3),(4,5),(4,6)
(5,1),(5,2)(5,3),(5,4),(5,6)
(6,1),(6,2)(6,3),(6,4),(6,5)
(Ⅰ)设A表示“甲、乙两单位的演出序号均为偶数”
则A包含如下6种基本事件:(2,4),(2,6),(4,2),(4,6),(6,2),(6,4)
据古典概型概率公式,故所求概率为
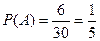
(Ⅱ)设B表示“甲、乙两单位的演出序号不相邻”
则
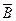 表示“甲、乙两单位的演出序号相邻”
表示“甲、乙两单位的演出序号相邻” 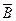 包含如
包含如 下10种基本事件:
下10种基本事件:(1,2),(2,3),(3,4),(4,5),(5,6)
(2,1),(3,2),(4,3),(5,4),(6,5),
据古典概型概率公式,从而所求概率为
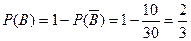
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 排放量超过
排放量超过 的
的 型新车进行惩罚.某检测单位对甲、乙两类
型新车进行惩罚.某检测单位对甲、乙两类 辆进行
辆进行 ).
).


 排放量的概率是多少?
排放量的概率是多少? ,试比较甲、乙两类品牌车
,试比较甲、乙两类品牌车 .如果用频率作为概率的估计值,并假定每一天发生雷电的概率均相等,且相互独立.
.如果用频率作为概率的估计值,并假定每一天发生雷电的概率均相等,且相互独立.
 ,求
,求 的次品率为
的次品率为 ,现在从
,现在从 件产品中任意的依次抽取
件产品中任意的依次抽取 件,分别以放回和不放回的方
件,分别以放回和不放回的方 式抽取,则恰有一件次品的概率分别为( )
式抽取,则恰有一件次品的概率分别为( )



 的游戏是
的游戏是  个球
个球