题目内容
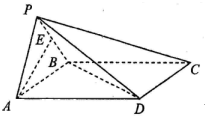四棱锥P-ABCD底面是平行四边形，面PAB⊥面ABCD，PA=PB=AB=| 1 |
| 2 |
（1）求证：AE⊥面PBD．
（2）设点M为线段PD上一点，且直线CM与平面PAD所成角的正弦值为
| ||
| 5 |
| PM |
| PD |
分析：（1）利用线面垂直的判定定理证明线面垂直．
（2）利用直线CM与平面PAD所成角的正弦值为
，确定M的位置，然后求
的值．
（2）利用直线CM与平面PAD所成角的正弦值为
| ||
| 5 |
| PM |
| PD |
解答：解：（1）因为AB=
AD，∠BAD=60°，所以AB⊥BD，
因为面PAB⊥面ABCD，面PAB∩面ABCD=AB，AB⊥BD，
所以BD⊥面PAB，所以BD⊥AE，
又PA=PB，E为PB的中点，
所以AE⊥PB，因为BD∩PB=B，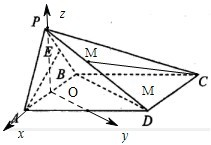
所以AE⊥面PBD．
（2）取AB的中点O，以O为坐标原点，以OA为x轴，OP为z轴，以平行BD的直线为y轴，建立空间直角坐标系，
设AB=2，则A（1，0，0），B（-1，0，0），P（0，0，
），D（-1，2
，0），C（-3，2
，0），则
=(-1，0
)，
=(-2，2
，0)，
=(-1，2
，-
)．，
=(-3，2
，-
)，所以
设平面PAD的法向量为
=(x，y，z)，则
，即
，令z=1，则x=
，y=1，
即
=(
，1，1)．
因为点M为线段PD上一点，设
=m，（0≤m≤1），则
=m
=(-m，2
m，-
m)，
=
+
=(m-3，2
-2
m，
m-
)，
因为直线CM与平面PAD所成角的正弦值为
，所以|cos＜
，
＞|=
．
即
=
，整理得8m2-18m+7=0，解得m=
或m=
（舍去）．
故
的值为
．
| 1 |
| 2 |
因为面PAB⊥面ABCD，面PAB∩面ABCD=AB，AB⊥BD，
所以BD⊥面PAB，所以BD⊥AE，
又PA=PB，E为PB的中点，
所以AE⊥PB，因为BD∩PB=B，
所以AE⊥面PBD．
（2）取AB的中点O，以O为坐标原点，以OA为x轴，OP为z轴，以平行BD的直线为y轴，建立空间直角坐标系，
设AB=2，则A（1，0，0），B（-1，0，0），P（0，0，
| 3 |
| 3 |
| 3 |
| AP |
| 3 |
| AD |
| 3 |
| PD |
| 3 |
| 3 |
| PC |
| 3 |
| 3 |
设平面PAD的法向量为
| n |
|
|
| 3 |
即
| n |
| 3 |
因为点M为线段PD上一点，设
| PM |
| PD |
| PM |
| PD |
| 3 |
| 3 |
| MC |
| MP |
| PC |
| 3 |
| 3 |
| 3 |
| 3 |
因为直线CM与平面PAD所成角的正弦值为
| ||
| 5 |
| n |
| MC |
| ||
| 5 |
即
|
| ||||
|
|
| ||
| 5 |
| 1 |
| 2 |
| 7 |
| 4 |
故
| PM |
| PD |
| 1 |
| 2 |
点评：本题主要考查线面垂直的判断，以及线面所成角的应用．建立空间直角坐标系，利用法向量是解决本题的关键，本题运算量较大，综合性较强．
练习册系列答案
相关题目
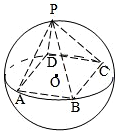如图，正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上，点P在球面上，若
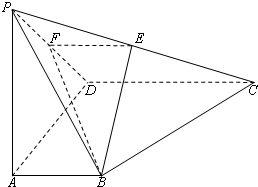如图所示，四棱锥P-ABCD底面是直角梯形，BA⊥AB，CD⊥DA，CD=2AB，PA⊥底面ABCD，E、F分别为PC，PD的中点，PA=AD=AB．
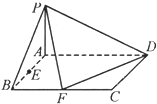已知四棱锥P-ABCD底面ABCD是矩形，PA丄平面ABCD，AD=4，AB=2，E，F分别是线段AB和BC的中点．
如图所示，四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，PA⊥底面ABCD，E为PC的中点，PA=AD=AB=1．
（2008•上海一模）如图，正四棱锥P-ABCD底面的四个顶点A，B，C，D在球O的同一个大圆上，点P在球面上，且已知