题目内容
【题目】已知![]() (
(![]() ).
).
(Ⅰ)判断当![]() 时
时![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,
,![]() (
(![]() )为
)为![]() 两个极值点,求证:
两个极值点,求证:![]() .
.
【答案】(Ⅰ)![]() 在定义域上为单调增函数;(Ⅱ)证明见解析.
在定义域上为单调增函数;(Ⅱ)证明见解析.
【解析】
(Ⅰ)先利用换元法求出![]() ,然后求函数的导数,结合函数单调性和导数的关系进行判断即可.
,然后求函数的导数,结合函数单调性和导数的关系进行判断即可.
(Ⅱ)根据极值的定义得到![]() 有两个不相等的正实数根
有两个不相等的正实数根![]() ,
,![]() ,利用根与系数之间的关系进行转化证明即可.
,利用根与系数之间的关系进行转化证明即可.
(Ⅰ)因为![]() (
(![]() ),
),
所以![]() ,(
,(![]() ).
).![]() ,
,
当![]() 时,
时,![]() ,
,![]() 恒成立.
恒成立.
于是,![]() 在定义域
在定义域![]() 上为单调增函数.
上为单调增函数.
(Ⅱ)证明:![]() ,
,
由题设知,![]() 有两个不相等的正实数根
有两个不相等的正实数根![]() ,
,![]() ,
,
则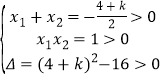 ,即
,即![]() ,得
,得![]()
而![]()
![]()
![]()
![]() ,
,
又![]() ,
,
故欲证原不等式等价于证明不等式:![]()
也就是要证明:对任意![]() ,有
,有![]()
令![]() ,由于
,由于![]() ,并且
,并且![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上为减函数;
上为减函数;
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上为增函数.
上为增函数.
则![]() 在
在![]() 上有最大值
上有最大值![]() ,即
,即![]() ,故原不等式成立.
,故原不等式成立.

【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早、晚读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成下表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为30%,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: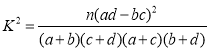 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】对于某种类型的口服药,口服![]() 小时后,由消化系统进入血液中药物浓度
小时后,由消化系统进入血液中药物浓度![]() (单位)与时间
(单位)与时间![]() 小时的关系为
小时的关系为![]() ,其中
,其中![]() ,
,![]() 为常数,对于某一种药物
为常数,对于某一种药物![]() ,
,![]() ,
,![]() .
.
(1)口服药物后______小时血液中药物浓度最高;
(2)这种药物服药![]() 小时后血液中药物浓度如下表
小时后血液中药物浓度如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0.9545 | 0.9304 | 0.6932 | 0.4680 | 0.3010 | 0.1892 | 0.1163 | 0.072 |
一个病人上午8:00第一次服药,要使得病人血液中药物浓度保持在0.5个单位以上,第三次服药时间是______(时间以整点为准)
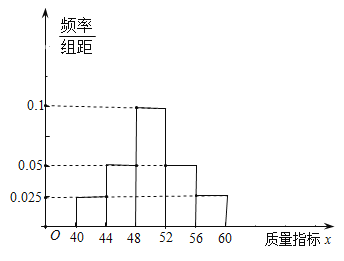
【题目】笔、墨、纸、砚是中国独有的文书工具,即文房四宝.笔、墨、纸、砚之名,起源于南北朝时期,其中“纸”指的是宣纸,“始于唐代,产于泾县”,因唐代泾县隶属宣州管辖,故因地得名宣纸,宣纸按质量等级分类可分为正牌和副牌(优等品和合格品)某公司生产的宣纸为纯手工制作,年产宣纸10000刀,该公司按照某种质量指标x给宣纸确定质量等级,如下表所示:
x的范围 |
|
|
|
质量等级 | 正牌 | 副牌 | 废品 |
公司在所生产的宣纸中随机抽取了一刀(100张)进行检验,得到的频率分布直方图如上图所示.已知每张正牌宣纸的利润为12元,副牌宣纸的利润为6元,废品宣纸的利润为-12元.
(1)试估计该公司生产宣纸的利润;
(2)该公司预备购买一种售价为100万元的机器改进生产工艺,这种机器使用寿命为一年,不影响产量,这种机器生产的宣纸的质量指标x服从正态分布![]() ,改进工艺后正牌和副牌宣纸的利润都将受到不同程度的影响,观测的数据如下表所示:
,改进工艺后正牌和副牌宣纸的利润都将受到不同程度的影响,观测的数据如下表所示:
x的范围 |
|
| ||
一张宣纸的利润 | 12 | 8 | 8 | 3 |
频率 | 0.5 | 0.5 | 0.5 | 0.5 |
将频率视为概率,请判断该公司是否应该购买这种机器,并说明理由
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【题目】某学校为进一步规范校园管理,强化饮食安全,提出了“远离外卖,健康饮食”的口号.当然,也需要学校食堂能提供安全丰富的菜品来满足同学们的需求.在学期末,校学生会为了调研学生对本校食堂A部和B部的用餐满意度,从在A部和B部都用过餐的学生中随机抽取了200人,每人分别对其评分,满分为100分.随后整理评分数据,将分数分成6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
,第6组![]() ,得到A部分数的频率分布直方图和B部分数的频数分布表.
,得到A部分数的频率分布直方图和B部分数的频数分布表.

分数区间 | 频数 |
| 7 |
| 18 |
| 21 |
| 24 |
| 70 |
| 60 |
定义:学生对食堂的“满意度指数”
分数 |
|
|
|
|
|
|
满意度指数 | 0 | 1 | 2 | 3 | 4 | 5 |
(1)求A部得分的中位数(精确到小数点后一位);
(2)A部为进一步改善经营,从打分在80分以下的前四组中,采用分层抽样的方法抽取8人进行座谈,再从这8人中随机抽取3人参与“端午节包粽子”实践活动,在第3组抽到1人的情况下,第4组抽到2人的概率;
(3)如果根据调研结果评选学生放心餐厅,应该评选A部还是B部(将频率视为概率)