题目内容
【题目】北京市某年11月1日—20日监测最高最低温度及差值数据如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高温度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低温度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的频率分布表及频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;

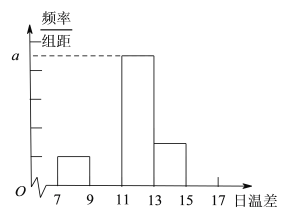
(Ⅱ)从日温差大于等于![]() 的这些天中,随机选取2天.求这两天中至少有一天的温差在区间
的这些天中,随机选取2天.求这两天中至少有一天的温差在区间![]() 内的概率.
内的概率.
【答案】(1)见解析;![]() .
.
(2)![]() .
.
【解析】
(1)利用题中所给的表格,求出每天的温差,数出落在![]() 内的频数,利用公式求得频率,完成频率分布表,完善直方图,利用直方图中长方形的面积等于对应的频率,求得
内的频数,利用公式求得频率,完成频率分布表,完善直方图,利用直方图中长方形的面积等于对应的频率,求得![]() 的值;
的值;
(2)先算出温差大于等于![]() 的天数,再找出温差在区间
的天数,再找出温差在区间![]() 内的天数,列出所有的基本事件,再数出满足条件的基本事件数,利用概率公式求得结果.
内的天数,列出所有的基本事件,再数出满足条件的基本事件数,利用概率公式求得结果.
(Ⅰ)

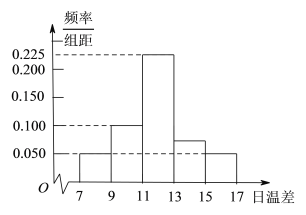
解得![]() .
.
(Ⅱ) 依题意,日温差在区间![]() 内的有3天,设为
内的有3天,设为![]() ;
;
气温差在![]() 内的有2天,设为
内的有2天,设为![]() .
.
则从日温差大于等于![]() 的这5天里随机抽取2天的基本事件空间为
的这5天里随机抽取2天的基本事件空间为
![]() 其包含的基本事件数
其包含的基本事件数![]() .
.
设事件![]() “两天中至少有一天的温差在区间
“两天中至少有一天的温差在区间![]() 内”.
内”. ![]() ,
,
其包含的基本事件数![]() .
.
则![]() .
.
所以这两天中至少有一天的温差在区间![]() 内的概率为
内的概率为![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目