题目内容
【题目】已知直线![]() :
:![]() 与抛物线
与抛物线![]() :
:![]()
(1)若直线![]() 与抛物线
与抛物线![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)若直线![]() 经过抛物线的焦点,且与抛物线相交于
经过抛物线的焦点,且与抛物线相交于![]() ,
,![]() 两点,当抛物线上一动点
两点,当抛物线上一动点![]() 从
从![]() 到
到![]() 运动时,求
运动时,求![]() 面积的最大值。
面积的最大值。
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由已知直线![]() 与抛物线对称轴不平行,因此可联立直线与抛物线的方程,消去
与抛物线对称轴不平行,因此可联立直线与抛物线的方程,消去![]() 得到关于
得到关于![]() 的一元二次方程,由此方程有唯一解,即
的一元二次方程,由此方程有唯一解,即![]() ,从而求出实数
,从而求出实数![]() 的值;(2)由题意,可将焦点弦
的值;(2)由题意,可将焦点弦![]() 作为
作为![]() 的底边,则点
的底边,则点![]() 到直线
到直线![]() 的距离
的距离![]() 就是
就是![]() 的高,而
的高,而![]() 已定,当
已定,当![]() 最大时,
最大时,![]() 的面积为最大,可设
的面积为最大,可设![]() 代入运算,求出
代入运算,求出![]() ,从而问题可得解.
,从而问题可得解.
试题解析:(1)由![]() ,因为直线
,因为直线![]() 与抛物线
与抛物线![]() 相切,
相切,
所以![]() 解得
解得![]()
(2)因为抛物线![]() 的焦点为(0,1),所以直线
的焦点为(0,1),所以直线![]() 方程为
方程为![]()
由![]() ,消去
,消去![]() ,得
,得![]() ,设
,设![]() ,则
,则
![]() ,
,
法一:![]() ,
,
法二:![]()
设![]() (
(![]() ),
),
因为![]() 为定值,当点
为定值,当点![]() 到直线
到直线![]() 的距离
的距离![]() 最大时,
最大时,![]() 面积的最大 ,
面积的最大 ,
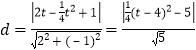 ,
,
![]()
![]() 当
当![]() 时,
时,![]()
所以![]() 面积的最大值为
面积的最大值为![]()

【题目】北京市某年11月1日—20日监测最高最低温度及差值数据如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高温度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低温度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的频率分布表及频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;

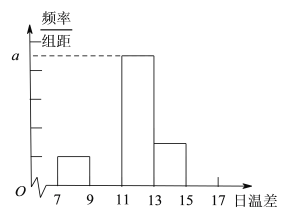
(Ⅱ)从日温差大于等于![]() 的这些天中,随机选取2天.求这两天中至少有一天的温差在区间
的这些天中,随机选取2天.求这两天中至少有一天的温差在区间![]() 内的概率.
内的概率.
【题目】为了增强消防安全意识,某中学对全体学生做了一次消防知识讲座,从男生中随机抽取50人,从女生中随机抽取70人参加消防知识测试,统计数据得到如下列联表:
优秀 | 非优秀 | 总计 | |
男生 | 15 | 35 | 50 |
女生 | 30 | 40 | 70 |
总计 | 45 | 75 | 120 |
(Ⅰ)试判断是否有![]() 的把握认为消防知识的测试成绩优秀与否与性别有关;
的把握认为消防知识的测试成绩优秀与否与性别有关;
附:
K2=![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅱ)为了宣传消防安全知识,从该校测试成绩获得优秀的同学中采用分层抽样的方法,随机选出6名组成宣传小组,现从这6人中随机抽取2名到校外宣传,求到校外宣传的同学中至少有1名是男生的概率.


