题目内容
【题目】已知函数![]() 在
在![]() 与
与![]() 时都取得极值;
时都取得极值;
(1)求![]() 的值与函数
的值与函数![]() 的单调区间;
的单调区间;
(2)若对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围
的取值范围
【答案】(1)a=![]() ,b=-2,递增区间是(-,-
,b=-2,递增区间是(-,- ![]() )与(1,+)递减区间是(-
)与(1,+)递减区间是(-![]() ,1)(2)c-1或c2
,1)(2)c-1或c2
【解析】 试题分析:(1)根据极值定义得f(![]() )=0,f(1)=0,解方程组可得
)=0,f(1)=0,解方程组可得![]() 的值,再列表根据导函数符号确定单调区间(2)不等式恒成立问题一般转化为对应函数最值问题:f(x)最大值c2,根据(1)可得f(x)最大值为f(2),解不等式可得
的值,再列表根据导函数符号确定单调区间(2)不等式恒成立问题一般转化为对应函数最值问题:f(x)最大值c2,根据(1)可得f(x)最大值为f(2),解不等式可得![]() 的取值范围
的取值范围
试题解析:解:(1)f(x)=x3+ax2+bx+c,f(x)=3x2+2ax+b
由f(![]() )=
)=![]() ,f(1)=3+2a+b=0得
,f(1)=3+2a+b=0得
a=![]() ,b=-2
,b=-2
f(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
x | (-,- | - | (- | 1 | (1,+) |
f(x) | + | 0 | - | 0 | + |
f(x) | 极大值 | 极小值 |
所以函数f(x)的递增区间是(-,- ![]() )与(1,+)
)与(1,+)
递减区间是(-![]() ,1)
,1)
(2)f(x)=x3-![]() x2-2x+c,x〔-1,2〕,当x=-
x2-2x+c,x〔-1,2〕,当x=-![]() 时,f(x)=
时,f(x)=![]() +c
+c
为极大值,而f(2)=2+c,则f(2)=2+c为最大值。
要使f(x)c2(x〔-1,2〕)恒成立,只需c2f(2)=2+c
解得c-1或c2

【题目】北京市某年11月1日—20日监测最高最低温度及差值数据如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高温度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低温度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的频率分布表及频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;

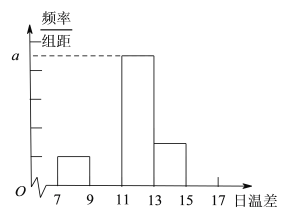
(Ⅱ)从日温差大于等于![]() 的这些天中,随机选取2天.求这两天中至少有一天的温差在区间
的这些天中,随机选取2天.求这两天中至少有一天的温差在区间![]() 内的概率.
内的概率.

