题目内容
已知 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
(1)证明:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1)证明详见解析; 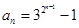 ;(2)
;(2) 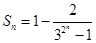
解析试题分析:(1)把点(an,an+1)代入f(x)=x2+2x中,整理可得递推公式an+1+1=(an+1)2,两边取常用对数,整理可证 是公比为2,a1=2的等比数列,然后由数列
是公比为2,a1=2的等比数列,然后由数列 的通项公式可推出数列{an}的通项公式.(2)由已知递推公式an+1=an2+2an变形整理得
的通项公式可推出数列{an}的通项公式.(2)由已知递推公式an+1=an2+2an变形整理得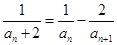 ,代入
,代入 中,整理可得
中,整理可得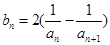 最后利用裂项法求数列的前n项和Sn.
最后利用裂项法求数列的前n项和Sn.
试题解析:(Ⅰ)由已知 ,
, 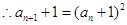
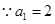
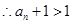 ,两边取对数得
,两边取对数得 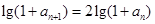 ,即
,即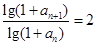
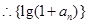 是公比为2的等比数列.
是公比为2的等比数列. 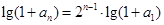
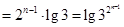
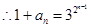 (*)
(*)
由(*)式得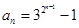
(2)
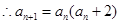
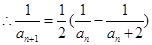
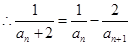
又
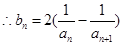
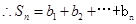
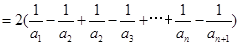
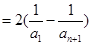
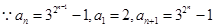
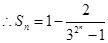 .
.
考点:1.数列的递推公式及等比数列的定义和通项公式;2.求数列的前n项和.

练习册系列答案
相关题目
 满足:
满足: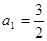 ,
, 
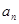 ;
; 满足
满足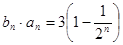 ,求数列
,求数列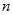 项和.
项和.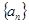 ,
,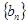 ,
,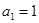 ,
,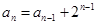 ,
,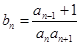 ,
, 为数列
为数列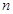 项和,
项和,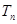 为数列
为数列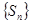 的前
的前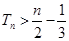 .
. 的前
的前 项和
项和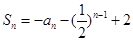 (
( ,求证数列
,求证数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,试比较
,试比较 与
与 的大小,并予以证明
的大小,并予以证明 的公差
的公差 大于0,且
大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项和为
项和为 .
. 的通项公式;
的通项公式; ,求证:
,求证: ;
; 的前
的前 .
. 满足
满足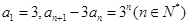 ,数列
,数列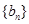 满足
满足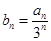 .
. 项和
项和 .
. 的前n项和为
的前n项和为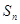 ,
,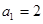 ,当n≥2时,
,当n≥2时, ,
, ,
, 成等差数列. (1)求数列
成等差数列. (1)求数列 的通项公式;
的通项公式; ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 .
. 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且 成等比数列。
成等比数列。 ,求
,求 ,
, 是数列
是数列 的前
的前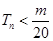 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。 x
x -
- x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.