��Ŀ����
8���趨����ΪR�ĺ���f��x��=$\left\{\begin{array}{l}{lo{g}_{2}��x+2����x��-1}\\{{x}^{2}+4x+4��x��-1}\end{array}\right.$����1����ƽ��ֱ����������������f��x����ͼ��ָ��f��x���ĵ������䣨����֤������
��2��������x�ķ���f��x��-2a=0����������ȵ�ʵ��������a��ȡֵ��Χ��ֻ���˵���������ϸ�֤������
��3����g��x��ΪR�ϵ��溯�����ҵ�x��0ʱ��g��x��=f��x������g��x���Ľ���ʽ��
���� ��1�����ݺ�������ʽ���ɵú�����ͼ�Ӷ��ɵú����ĵ������䣻
��2����ͬһ����ϵ��ͬʱ����y=f��x����y=2aͼ����ͼ��֪f��x��-2a=0�������⣬��2a=0��2a��1���Ӷ�����a��ȡֵ��Χ��
��3�����x��0ʱ�������Ľ���ʽ���������g��x���Ľ���ʽ��
��� 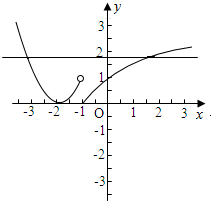 �� ��1����ͼ������3�֣�
�� ��1����ͼ������3�֣�
�������䣺[-2��-1����[-1��+�ޣ��������䣨-�ޣ�-2]������5�֣�
��2����ͬһ����ϵ��ͬʱ����y=f��x����y=2aͼ����ͼ��֪f��x��-2a=0��������
��2a=0��2a��1����a=0��a��$\frac{1}{2}$ ����8�֣�
��3����x��0ʱ��-x��0����g��-x��=log2��-x+2����
��Ϊg��x��Ϊ�溯��������g��x��=-log2��-x+2��������10�֣�
��g��0��=0������g��x��=$\left\{\begin{array}{l}{lo{g}_{2}��x+2����x��0}\\{0��x=0}\\{-lo{g}_{2}��-x+2����x��0}\end{array}\right.$����12�֣�
���� ���⿼��ֶκ��������ã����麯����ͼ�������ν�ϵ���ѧ˼�룬��ȷ���ú�����ͼ���ǹؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
20������˵����ȷ���� ��������
| A�� | ��֪F1��-4��0����F2��4��0����������F1��F2�ľ���֮�ʹ���8�ĵ�Ĺ켣����Բ | |
| B�� | ��֪F1��-4��0����F2��4��0����������F1��F2�ľ���֮�͵���6�ĵ�Ĺ켣����Բ | |
| C�� | ����F1��-4��0����F2��4��0���ľ���֮�͵��ڴӵ㣨5��3����F1��F2�ľ���֮�͵ĵ�Ĺ켣����Բ | |
| D�� | ����F1��-4��0����F2��4.0��������ȵĵ�Ĺ켣����Բ |