题目内容
给出下列四个命题:
①函数f(x)=lnx-2+x在区间(1,e)上存在零点;
②若f′(x0)=0,则函数y=f(x)在x=x0处取得极值;
③若m≥-1,则函数y=log
(x2-2x-m)的值域为R;
④已知x1是方程x+lgx=5的根,x2是方程x+10x=5的根,则x1+x2=5.
其中正确的序号是
①函数f(x)=lnx-2+x在区间(1,e)上存在零点;
②若f′(x0)=0,则函数y=f(x)在x=x0处取得极值;
③若m≥-1,则函数y=log
| 1 | 2 |
④已知x1是方程x+lgx=5的根,x2是方程x+10x=5的根,则x1+x2=5.
其中正确的序号是
①③④
①③④
.分析:①利用零点存在定理判断即可;
②举例说明,令f(x)=x3,f′(0)=0,判断即可;
③令g(x)=x2-2x-m,依题意,方程x2-2x-m=0有实根,从而可求得m;
④利用y=lgx与y=10x互为反函数,它们的图象关于直线y=x对称,判断即可.
②举例说明,令f(x)=x3,f′(0)=0,判断即可;
③令g(x)=x2-2x-m,依题意,方程x2-2x-m=0有实根,从而可求得m;
④利用y=lgx与y=10x互为反函数,它们的图象关于直线y=x对称,判断即可.
解答: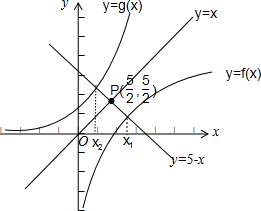 解:①∵f(x)=lnx-2+x在(1,e)上连续不断,且f(1)=-1<0,f(e)=e-1>0,
解:①∵f(x)=lnx-2+x在(1,e)上连续不断,且f(1)=-1<0,f(e)=e-1>0,
∴函数f(x)=lnx-2+x在区间(1,e)上存在零点,即①正确;
②不妨令f(x)=x3,则f′(x)=3x2≥0,
∴f(x)=x3在R上单调递增,无极值,而f′(0)=0,
∴②若f′(x0)=0,则函数y=f(x)在x=x0处取得极值,错误;
③令g(x)=x2-2x-m,依题意,方程x2-2x-m=0有实根,
∴△=(-2)2-4×(-m)=4+4m≥0,
∴m≥-1,故③正确;
对于④,方程方程x+lgx=5和方程x+10x=5的可化为方程lgx=5-x和方程10x=5-x,
令f(x)=lgx,g(x)=10x,y=5-x,画图:
显然x1是函数f(x)=lgx 与 y=5-x图象的交点的横坐标,
x2是函数g(x)=10x与 y=5-x的图象的交点的横坐标,
由于函数 f(x)=lgx与g(x)=10x的图象关于y=x对称,直线y=5-x也关于y=x 对称,且直线 y=5-x与它们都只有一个交点,
∴这两个交点关于y=x对称.又因为两个交点的中点P是y=5-x与y=x 的交点,即P(
,
),
∴x1+x2=2×
=5,
∴④正确.
∴正确的序号是①③④.
故答案为:①③④.
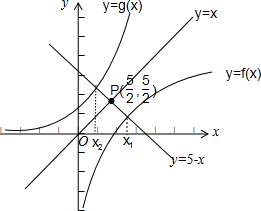 解:①∵f(x)=lnx-2+x在(1,e)上连续不断,且f(1)=-1<0,f(e)=e-1>0,
解:①∵f(x)=lnx-2+x在(1,e)上连续不断,且f(1)=-1<0,f(e)=e-1>0,∴函数f(x)=lnx-2+x在区间(1,e)上存在零点,即①正确;
②不妨令f(x)=x3,则f′(x)=3x2≥0,
∴f(x)=x3在R上单调递增,无极值,而f′(0)=0,
∴②若f′(x0)=0,则函数y=f(x)在x=x0处取得极值,错误;
③令g(x)=x2-2x-m,依题意,方程x2-2x-m=0有实根,
∴△=(-2)2-4×(-m)=4+4m≥0,
∴m≥-1,故③正确;
对于④,方程方程x+lgx=5和方程x+10x=5的可化为方程lgx=5-x和方程10x=5-x,
令f(x)=lgx,g(x)=10x,y=5-x,画图:
显然x1是函数f(x)=lgx 与 y=5-x图象的交点的横坐标,
x2是函数g(x)=10x与 y=5-x的图象的交点的横坐标,
由于函数 f(x)=lgx与g(x)=10x的图象关于y=x对称,直线y=5-x也关于y=x 对称,且直线 y=5-x与它们都只有一个交点,
∴这两个交点关于y=x对称.又因为两个交点的中点P是y=5-x与y=x 的交点,即P(
| 5 |
| 2 |
| 5 |
| 2 |
∴x1+x2=2×
| 5 |
| 2 |
∴④正确.
∴正确的序号是①③④.
故答案为:①③④.
点评:本题考查命题的真假判断与应用,着重考查零点存在定理、极值的概念、对数函数的性质及反函数,属于中档题.

练习册系列答案
相关题目