题目内容
 设F1、F2分别是椭圆C:
设F1、F2分别是椭圆C:| x2 |
| 6m2 |
| y2 |
| 2m2 |
(I)当p∈C,且
| pF1 |
| pF |
| pF1 |
| pF |
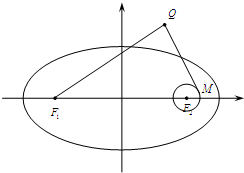
(II)F1、F2是(I)中的椭圆的左、右焦点,已知⊙F2的半径是1,过动点Q作的切线QM(M为切点),使得|QF1|=
| 2 |
分析:(I)由
•
=0,知PF12+PF22=16m2,由|
|•|
|=4,知(PF1+PF2)2-8=16m2,由此能求出椭圆C的左、右焦点F1、F2的坐标.
(II)设Q(x,y),连接QF2及F2M,由QM与⊙F2的切线,知QM2=(x-1)2+y2-1.由|QF1|=
|QM|,知(x+2)2+y2=2[(x-2)2+y2-1].由此能求出动点Q的轨迹.
| PF1 |
| PF2 |
| PF1 |
| PF2 |
(II)设Q(x,y),连接QF2及F2M,由QM与⊙F2的切线,知QM2=(x-1)2+y2-1.由|QF1|=
| 2 |
解答:解:(I)∵
•
=0
∴PF12+PF22=F1F22
∴PF12+PF22=16m2…(2分)
又∵|
|•|
|=4
∴(PF1+PF2)2-8=16m2…(4分)
∴m2=1…(6分)
∴F1(-2,0)F2(2,0)…(7分)
(II)Q(x,y)
连接QF2及F2M
∵QM与⊙F2的切线
∴QM2=QF22-F2M2…(9分)
∴QM2=(x-1)2+y2-1…(10分)
又∵|QF1|=
|QM|
∴|QF1|2=2|QM|2…(12分)
∴(x+2)2+y2=2[(x-2)2+y2-1]…(13分)
∴(x-6)2+y2=34…(15分)
∴动点Q的轨迹是以(6,0)为圆心,
为半径的圆…(16分)
| PF1 |
| PF2 |
∴PF12+PF22=F1F22
∴PF12+PF22=16m2…(2分)
又∵|
| PF1 |
| PF2 |
∴(PF1+PF2)2-8=16m2…(4分)
∴m2=1…(6分)
∴F1(-2,0)F2(2,0)…(7分)
(II)Q(x,y)
连接QF2及F2M
∵QM与⊙F2的切线
∴QM2=QF22-F2M2…(9分)
∴QM2=(x-1)2+y2-1…(10分)
又∵|QF1|=
| 2 |
∴|QF1|2=2|QM|2…(12分)
∴(x+2)2+y2=2[(x-2)2+y2-1]…(13分)
∴(x-6)2+y2=34…(15分)
∴动点Q的轨迹是以(6,0)为圆心,
| 34 |
点评:本题考查椭圆的左、右焦点坐标的求法和求动点的轨迹.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
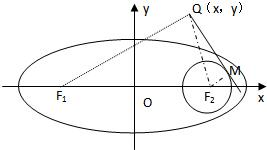 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C: