题目内容
设F1,F2分别是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
(Ⅰ)求此椭圆方程;
(Ⅱ)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N,且线段MN的垂直平分线过定点G(
| 1 |
| 8 |
分析:(Ⅰ)由已知得到关于a,b的两个方程,解出对应a,b的值即可.
(Ⅱ)先把直线方程与椭圆方程联立,找到关于点M、N的中点坐标,把其代入线段MN的垂直平分线方程,可以得到k和m之间的一个等量关系,再利用直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N,对应判别式大于0,就可求出k的取值范围.
(Ⅱ)先把直线方程与椭圆方程联立,找到关于点M、N的中点坐标,把其代入线段MN的垂直平分线方程,可以得到k和m之间的一个等量关系,再利用直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N,对应判别式大于0,就可求出k的取值范围.
解答:解:(Ⅰ)由题意有
,解得
∴椭圆的方程为
+
=1
(Ⅱ)设M(x1,y1),N(x2,y2),由
?(3+4k2)x2+8kmx+4m2-12=0
∵直线y=kx+m与椭圆有两个交点
∴△=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3
又x1+x2=-
∴MN中点P的坐标为(-
,
)
设MN的垂直平分线l'方程:y=-
(x-
)
∵p在l'上∴
=-
(-
-
)
即4k2+8km+3=0∴m=-
(4k2+3)
将上式代入得
<4k2+3∴k2>
即k>
或k<-
∴k的取值范围为(-∞,-
)∪(
,+∞).
|
|
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设M(x1,y1),N(x2,y2),由
|
∵直线y=kx+m与椭圆有两个交点
∴△=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3
又x1+x2=-
| 8km |
| 3+4k2 |
| 4km |
| 3+4k2 |
| 3m |
| 3+4k2 |
设MN的垂直平分线l'方程:y=-
| 1 |
| k |
| 1 |
| 8 |
∵p在l'上∴
| 3m |
| 3+4k2 |
| 1 |
| k |
| 4km |
| 3+4k2 |
| 1 |
| 8 |
即4k2+8km+3=0∴m=-
| 1 |
| 8k |
将上式代入得
| (4k2+3)2 |
| 64k2 |
| 1 |
| 20 |
即k>
| ||
| 10 |
| ||
| 10 |
| ||
| 10 |
| ||
| 10 |
点评:本题综合考查了直线与椭圆的位置关系以及椭圆标准方程的求法问题.在求椭圆的标准方程时,用定义是常用的方法.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
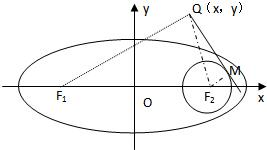 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C: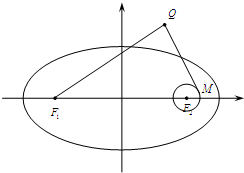 设F1、F2分别是椭圆
设F1、F2分别是椭圆