题目内容
1.已知椭圆M:$\frac{x^2}{4}+\frac{y^2}{3}$=1,点F1,C分别是椭圆M的左焦点、左顶点,过点F1的直线l(不与x轴重合)交M于A,B两点.(Ⅰ)求M的离心率及短轴长;
(Ⅱ)是否存在直线l,使得点B在以线段AC为直径的圆上,若存在,求出直线l的方程;若不存在,说明理由.
分析 (Ⅰ)通过椭圆M方程:$\frac{x^2}{4}+\frac{y^2}{3}=1$,直接计算即可;
(Ⅱ)通过设B(x0,y0)(-2<x0<2),利用$\overrightarrow{B{F}_{1}}$•$\overrightarrow{BC}$>0可得$∠B∈(0,\frac{π}{2})$,进而可得结论.
解答 解:(Ⅰ)由$\frac{x^2}{4}+\frac{y^2}{3}=1$,得:$a=2,b=\sqrt{3}$,
∴椭圆M的短轴长为$2\sqrt{3}$,
∴$c=\sqrt{{a^2}-{b^2}}=1$,
∴$e=\frac{c}{a}=\frac{1}{2}$,即M的离心率为$\frac{1}{2}$;
(Ⅱ)结论:不存在直线l,使得点B在以AC为直径的圆上.
理由如下:
由题意知:C(-2,0),F1(-1,0),
设B(x0,y0)(-2<x0<2),则$\frac{x_0^2}{4}+\frac{y_0^2}{3}=1$.
∵$\overrightarrow{B{F_1}}•\overrightarrow{BC}=(-1-{x_0},-{y_0})•(-2-{x_0},-{y_0})$
=$2+3{x_0}+x_0^2+y_0^2$
=$\frac{1}{4}x_0^2+3{x_0}+5>0$,
∴cos∠F1BC>0,
∴∠F1BC为锐角,即$∠B∈(0,\frac{π}{2})$,
∴点B不在以AC为直径的圆上,即:不存在直线l,使得点B在以AC为直径的圆上.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
14.已知命题p函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+x有两个极值点;命题q:函数g(x)=x${\;}^{{a}^{2}-a}$在(0,+∞)上为增函数,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知x,y∈R,则“x>y”是“|x|>|y|”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
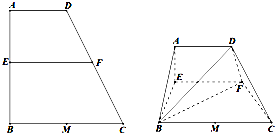 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.