题目内容
点P在双曲线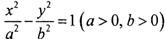 上•,
上•,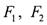 是这条双曲线的两个焦点,
是这条双曲线的两个焦点, ,且
,且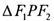 的三条边长成等差数列,则此双曲线的离心率是
的三条边长成等差数列,则此双曲线的离心率是
5
解析试题分析:设P是双曲线右支上一点,由三条边长成等差数列得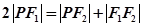
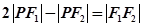 ,即
,即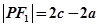
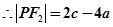 因为
因为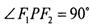 所以有
所以有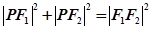 代入整理得
代入整理得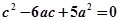
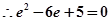
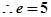
考点:双曲线定义及离心率
点评:双曲线定义:双曲线上的点到两焦点的距离之差的绝对值等于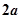 ,求离心率的题目关键是找到关于
,求离心率的题目关键是找到关于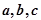 的齐次方程或不等式
的齐次方程或不等式

练习册系列答案
相关题目
题目内容
点P在双曲线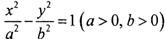 上•,
上•,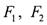 是这条双曲线的两个焦点,
是这条双曲线的两个焦点, ,且
,且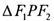 的三条边长成等差数列,则此双曲线的离心率是
的三条边长成等差数列,则此双曲线的离心率是
5
解析试题分析:设P是双曲线右支上一点,由三条边长成等差数列得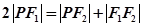
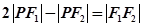 ,即
,即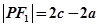
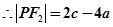 因为
因为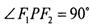 所以有
所以有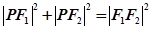 代入整理得
代入整理得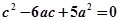
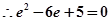
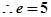
考点:双曲线定义及离心率
点评:双曲线定义:双曲线上的点到两焦点的距离之差的绝对值等于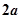 ,求离心率的题目关键是找到关于
,求离心率的题目关键是找到关于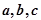 的齐次方程或不等式
的齐次方程或不等式
