题目内容
已知直线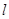 经过椭圆
经过椭圆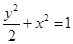 的焦点并且与椭圆相交于
的焦点并且与椭圆相交于 ,
,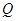 两点,线段
两点,线段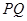 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点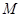 ,则
,则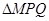 面积的最大值为 .
面积的最大值为 .
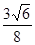
解析试题分析:设椭圆上焦点为F,则S△MPQ=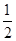 •|FM|•|x1-x2|=
•|FM|•|x1-x2|=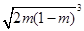 ,所以△MPQ的面积为
,所以△MPQ的面积为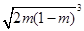 (0<m<
(0<m<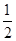 )
)
设f(m)=m(1-m)3,则f'(m)=(1-m)2(1-4m)(0,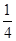 )
)
可知f(m)在区间(0,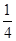 )单调递增,在区间(
)单调递增,在区间(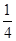 ,
,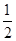 )单调递减.
)单调递减.
所以,当(0,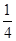 )时,f(m)=m(1-m)3有最大值f(
)时,f(m)=m(1-m)3有最大值f(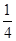 )=
)=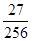
所以,当时,△MPQ的面积有最大值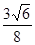
考点:本试题考查了椭圆的性质,以及三角形面积知识。
点评:解决该题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,属于中档题。

练习册系列答案
相关题目
已知函数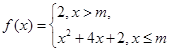 的图像与直线
的图像与直线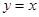 恰有三个公共点,则实数m的取值范围是( )
恰有三个公共点,则实数m的取值范围是( )
A.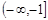 | B.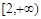 | C.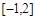 | D.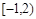 |
 到点
到点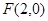 的距离与它到直线
的距离与它到直线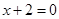 的距离相等,则点
的距离相等,则点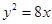 上,点Q在曲线C2:(x-2)2+y2=1上,点O为坐标原点,则
上,点Q在曲线C2:(x-2)2+y2=1上,点O为坐标原点,则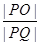 的最大值是 .
的最大值是 .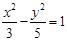 的左焦点F引圆
的左焦点F引圆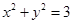 的切线FP交双曲线右支于点P,T为切点,M为线段FP的中点,O为坐标原点,则| MO | – | MT | = .
的切线FP交双曲线右支于点P,T为切点,M为线段FP的中点,O为坐标原点,则| MO | – | MT | = .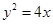 的焦点, A、B是抛物线上两点,若
的焦点, A、B是抛物线上两点,若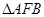 是正三角形,则
是正三角形,则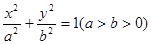 的左、右准线分别为
的左、右准线分别为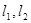 ,且分别交
,且分别交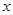 轴于
轴于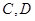 两点,从
两点,从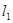 上一点
上一点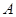 发出一条光线经过椭圆的左焦点
发出一条光线经过椭圆的左焦点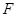 被
被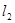 交于点
交于点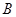 ,若
,若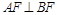 ,且
,且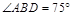 ,则椭圆的离心率等于 .
,则椭圆的离心率等于 .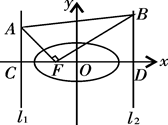
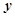 轴上,虚轴长为8,焦距为10的双曲线的标准方程是 ;
轴上,虚轴长为8,焦距为10的双曲线的标准方程是 ;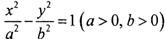 上•,
上•,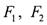 是这条双曲线的两个焦点,
是这条双曲线的两个焦点, ,且
,且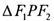 的三条边长成等差数列,则此双曲线的离心率是
的三条边长成等差数列,则此双曲线的离心率是