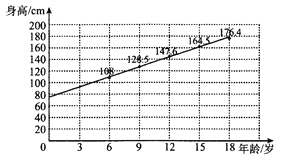
题目内容
【题目】如图,四棱锥P﹣ABCD的底面是矩形,PA⊥底面ABCD,PA=AD,点E、F分别为棱AB、PD的中点. (Ⅰ)求证:AF∥平面PCE;
(Ⅱ)AD与平面PCD所成的角的大小.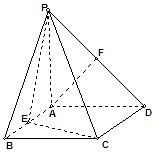
【答案】解:(Ⅰ)证明:取PC的中点G,连结FG、EG, 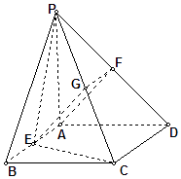
∴FG为△CDP的中位线,
∴FG ![]() CD,
CD,
∵四边形ABCD为矩形,E为AB的中点,
∴AE ![]() CD,
CD,
∴FG ![]() AE,
AE,
∴四边形AEGF是平行四边形,
∴AF∥EG又EG平面PCE,
AF平面PCE,
∴AF∥平面PCE;
(Ⅱ)∵PA⊥底面ABCD,
∴PA⊥AD,PA⊥CD,
又AD⊥CD,PA∩AD=A,
∴CD⊥平面ADP
又AF平面ADP,
∴CD⊥AF
在直角三角形PAD中,PA=AD且F是PD的中点,
∴AF⊥PD,
又CD∩PD=D,
∴AF⊥平面PCD.
∴∠ADP就是AD与平面PCD所成的角.
在直角三角形PAD中,PA=AD,
∴∠PDA=45°
∴AD与平面PCD所成的角是45°.
【解析】(Ⅰ)取PC的中点G,连结FG、EG,则FG ![]() CD,AE
CD,AE ![]() CD,因此FG
CD,因此FG ![]() AE,AF∥EG又EG平面PCE,AF平面PCE,AF∥平面PCE;(Ⅱ)PA⊥底面ABCD,可证明CD⊥平面ADP,CD⊥AF,则AF⊥PD,AF⊥平面PCD,∠ADP就是AD与平面PCD所成的角,PA=AD,∠PDA=45°.
AE,AF∥EG又EG平面PCE,AF平面PCE,AF∥平面PCE;(Ⅱ)PA⊥底面ABCD,可证明CD⊥平面ADP,CD⊥AF,则AF⊥PD,AF⊥平面PCD,∠ADP就是AD与平面PCD所成的角,PA=AD,∠PDA=45°.
【考点精析】掌握直线与平面平行的判定和空间角的异面直线所成的角是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则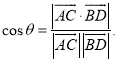 .
.

练习册系列答案
相关题目