题目内容
已知函数f(x)=x3-x2+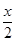 +
+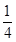 .
.
证明:存在x0∈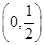 ,使f(x0)=x0.
,使f(x0)=x0.
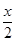 +
+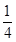 .
.证明:存在x0∈
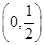 ,使f(x0)=x0.
,使f(x0)=x0.见解析
证明:令g(x)=f(x)-x.
∵g(0)=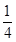 ,
,
g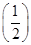 =f
=f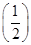 -
-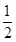 =-
=- ,
,
∴g(0)·g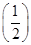 <0.
<0.
又函数g(x)在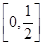 上连续,
上连续,
∴存在x0∈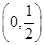 ,使g(x0)=0,
,使g(x0)=0,
即f(x0)=x0.
∵g(0)=
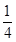 ,
,g
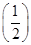 =f
=f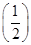 -
-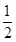 =-
=- ,
,∴g(0)·g
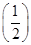 <0.
<0.又函数g(x)在
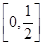 上连续,
上连续,∴存在x0∈
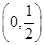 ,使g(x0)=0,
,使g(x0)=0,即f(x0)=x0.

练习册系列答案
相关题目
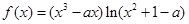 (
(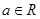 )
)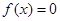 有3个不同的根,求实数
有3个不同的根,求实数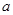 的取值范围;
的取值范围;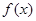 在
在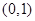 上恰有两个极值点
上恰有两个极值点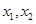 ,且满足
,且满足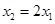 ,若存在,求实数
,若存在,求实数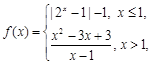 函数
函数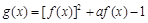 (其中a为常数),给出下列结论:
(其中a为常数),给出下列结论: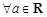 ,函数
,函数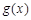 至少有一个零点;
至少有一个零点; ,函数
,函数
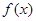 的定义域[-1,5],部分对应值如表,
的定义域[-1,5],部分对应值如表, 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数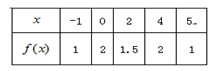
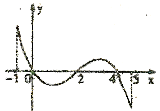
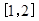 ;
; 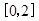 上是减函数;
上是减函数;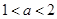 时,函数
时,函数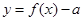 最多有4个零点;
最多有4个零点;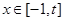 时,
时,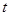 的最大值为4.
的最大值为4.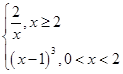 ,若关于x的方程f(x)=kx有两个不同的实根,则实数k的取值范围是________.
,若关于x的方程f(x)=kx有两个不同的实根,则实数k的取值范围是________.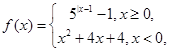 若关于x的方程
若关于x的方程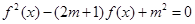 有7个不同的实数解,则m=( ).
有7个不同的实数解,则m=( ).