题目内容
在平面直角坐标系中,曲线C: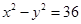 经过伸缩变换
经过伸缩变换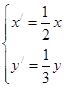 后,所得曲线的焦点坐标为( ).
后,所得曲线的焦点坐标为( ).
A.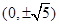 | B.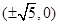 | C.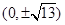 | D.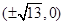 |
D
解析试题分析:由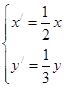 得
得 ;代入
;代入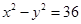 ,得
,得 ;即所得曲线方程为
;即所得曲线方程为 ,所以
,所以 ,即所得曲线的焦点坐标为
,即所得曲线的焦点坐标为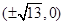 .
.
考点:曲线的变换.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( )
| A.θ=0(ρ∈R)和ρcos θ=2 | B.θ=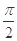 (ρ∈R)和ρcos θ=2 (ρ∈R)和ρcos θ=2 |
C.θ=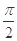 (ρ∈R)和ρcos θ=1 (ρ∈R)和ρcos θ=1 | D.θ=0(ρ∈R)和ρcos θ=1 |
过点且平行于极轴的直线的极坐标方程是( )
| A.ρcosθ=4 | B.ρsinθ=4 | C.ρsinθ=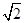 | D.ρcosθ=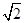 |
极坐标系中,由三条曲线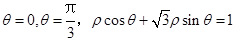 围成的图形的面积是( )
围成的图形的面积是( )
A.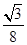 | B.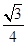 | C.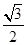 | D.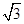 |
在极坐标系中,圆C过极点,且圆心的极坐标是 (
( ),则圆C的极坐标方程是( )
),则圆C的极坐标方程是( )
A. . . | B. . . | C. . . | D.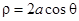 . . |

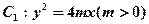 的准线与x轴交于点
的准线与x轴交于点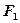 ,
,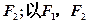 为焦点,离心率为
为焦点,离心率为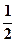 的椭圆
的椭圆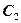 与抛物线
与抛物线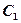 在x轴上方的交点为P
在x轴上方的交点为P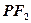 交抛物线于点Q,M是抛物线
交抛物线于点Q,M是抛物线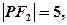 且P点横坐标为
且P点横坐标为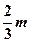 ,求面积
,求面积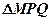 的最大值
的最大值
 =2sin(
=2sin( +
+ )的图形是( )
)的图形是( )
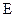 的中心是坐标原点,焦点在坐标轴上,且椭圆过点
的中心是坐标原点,焦点在坐标轴上,且椭圆过点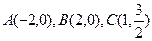 三点.
三点.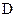 为椭圆
为椭圆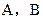 的任意一点,
的任意一点,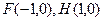 ,求
,求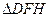 内切圆的面积的最大值,并指出其内切圆圆心的坐标.
内切圆的面积的最大值,并指出其内切圆圆心的坐标.