题目内容
20.若椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1的弦过点P(3,2),且被点P平分,求此弦所在直线的方程.分析 设出弦的两个端点,然后利用点差法求得弦所在直线的斜率,然后利用直线方程的点斜式得答案.
解答 解:设弦的两个端点分别为:A(x1,y1),B(x2,y2),
则$\frac{{{x}_{1}}^{2}}{36}+\frac{{{y}_{1}}^{2}}{16}=1$,$\frac{{{x}_{2}}^{2}}{36}+\frac{{{y}_{2}}^{2}}{16}=1$.
两式作差得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{36}=-\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{16}$.
∵点P(3,2)是弦AB的中点,
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-\frac{16}{36}•\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}=-\frac{4}{9}×\frac{6}{4}=-\frac{2}{3}$.
∴弦所在的直线方程为y-2=$-\frac{2}{3}$(x-3),即2x+3y-12=0.
点评 本题考查了椭圆的简单几何性质,考查了利用“点差法”求中点弦所在的直线方程,是中档题.

练习册系列答案
相关题目
5.函数f(x)=log2|-2x+a|在区间(3,4)上单调,则a的取值范围是( )
| A. | (6,8) | B. | [8,+∞) | C. | (-∞,6)∪(8,+∞) | D. | (-∞,6]∪[8,+∞) |
12.如图,正方形A1BCD折成直二面角A-BD-C,则二面角A-CD-B的余弦值是( )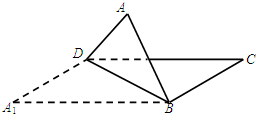

| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
9.已知函数f(x)=2|xsinx|,则函数f(x)在区间[-2π,2π]上的零点个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |