题目内容
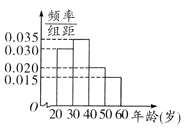
【题目】某工厂有120名工人,其年龄都在20~ 60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60]分成四组,其频率分布直方图如下图所示.工厂为了开发新产品,引进了新的生产设备。现采用分层抽样法从全厂工人中抽取一个容量为20的样本参加新设备培训,培训结束后进行结业考试。已知各年龄段培训结业考试成绩优秀的人数如下表所示:

若随机从年龄段[20,30)和[40,50)的参加培训工人中各抽取1人,则这两人培训结业考试成绩恰有一人优秀的概率为___________.
【答案】![]()
【解析】分析:由频率分布直方图计算出年龄段[20,30)和[40,50)的人数,各选一人得基本事件总数,再分两种情况计算恰有一个优秀的事件个数,作比即为概率.
详解:由频率分布直方图可知,年龄段[20,30),[30,40),[40,50),[50,60]的人数的频率分别为0.3,0.35,0.2,0.15,所以年龄段[20,30),[30,40),[40,50),[50,60]应抽取人数分别为6,7,4,3.
若随机从年龄段[20,30)和[40,50)的参加培训工人中各抽取1人,则这两人培训结业考试成绩恰有一人优秀的概率为![]() .
.
故答案为:![]() .
.

【题目】经销商第一年购买某工厂商品的单价为![]() (单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
(单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
上一年度 销售额/万元 |
|
|
|
|
|
|
商品单价/元 |
|
|
|
|
|
|
为了研究该商品购买单价的情况,为此调查并整理了![]() 个经销商一年的销售额,得到下面的柱状图.
个经销商一年的销售额,得到下面的柱状图.
已知某经销商下一年购买该商品的单价为![]() (单位:元),且以经销商在各段销售额的频率作为概率.
(单位:元),且以经销商在各段销售额的频率作为概率.
(1)求![]() 的平均估计值.
的平均估计值.
(2)为了鼓励经销商提高销售额,计划确定一个合理的年度销售额![]() (单位:万元),年销售额超过
(单位:万元),年销售额超过![]() 的可以获得红包奖励,该工厂希望使
的可以获得红包奖励,该工厂希望使![]() 的经销商获得红包,估计
的经销商获得红包,估计![]() 的值,并说明理由.
的值,并说明理由.