题目内容
【题目】已知集合P＝{x|x2－8x－20≤0}，S＝{x||x－1|≤m}．
(1)若(P∪S)P，求实数m的取值范围；
(2)是否存在实数m，使得“x∈P”是“x∈S”的充要条件？若存在，求出m的取值范围；若不存在，请说明理由．
【答案】（1）(－∞，3] （2）不存在，见解析
【解析】解：由x2－8x－20≤0解得－2≤x≤10，∴P＝{x|－2≤x≤10}．
由|x－1|≤m可得1－m≤x≤1＋m，∴S＝{x|1－m≤x≤1＋m}．
(1)要使(P∪S)P，则SP，
①若S＝，此时，m<0.
②若S≠，此时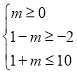
，解得0≤m≤3.
综合①②知实数m的取值范围为(－∞，3]．
(2)由题意“x∈P”是“x∈S”的充要条件，则S＝P，
则
∴
∴这样的m不存在．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某研究所计划利用宇宙飞船进行新产品搭载试验,计划搭载若干件新产品A,B,该研究所要根据产品的研制成本、产品重量、搭载试验费用和预计收益来决定具体安排,通过调查得到的有关数据如表:
每件A产品 | 每件B产品 | |
研制成本、搭载试验 费用之和(万元) | 20 | 30 |
产品重量(千克) | 10 | 5 |
预计收益(万元) | 80 | 60 |
已知研制成本、搭载试验费用之和的最大资金为300万元,最大搭载重量为110千克,则如何安排这两种产品进行搭载,才能使总预计收益达到最大,求最大预计收益是多少.
【题目】某学校要定制高一年级的校服，学生根据厂家提供的参考身高选择校服规格.据统计，高一年级女生需要不同规格校服的频数如表所示.
校服规格 | 155 | 160 | 165 | 170 | 175 | 合计 |
频数 | 39 | 64 | 167 | 90 | 26 | 386 |
如果用一个量来代表该校高一年级女生所需校服的规格，那么在中位数、平均数和众数中，哪个量比较合适？试讨论用表中的数据估计全国高一年级女生校服规格的合理性.
