题目内容
已知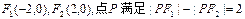
，记点P的轨迹为E.
（1）求轨迹E的方程；
（2）设直线l过点F2且与轨迹E交于P、Q两点，若无论直线l绕点F2怎样转动，在x轴上总存在定点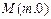
，使
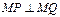恒成立，求实数m的值.
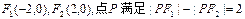，记点P的轨迹为E.（1）求轨迹E的方程；
（2）设直线l过点F2且与轨迹E交于P、Q两点，若无论直线l绕点F2怎样转动，在x轴上总存在定点
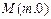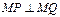，使恒成立，求实数m的值.解：（1）由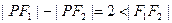
知，点P的轨迹E是以F1、F2为焦点的双曲线右支，由
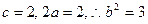，故轨迹E的方程为
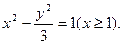（4分）
（2）当直线l的斜率存在时，设直线方程为
，与双曲线方程联立消y得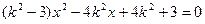
，
解得k2 >3
，
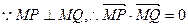故得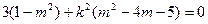
对任意的
恒成立，
∴当m =－1时，MP⊥MQ.
当直线l的斜率不存在时，由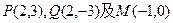
知结论也成立，
综上，当m =－1时，MP⊥MQ.
（11分）
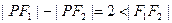知，点P的轨迹E是以F1、F2为焦点的双曲线右支，由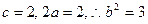，故轨迹E的方程为 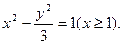（4分）（2）当直线l的斜率存在时，设直线方程为
，与双曲线方程联立消y得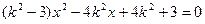，解得k2 >3
|
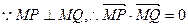，故得
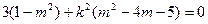对任意的恒成立，∴当m =－1时，MP⊥MQ.
当直线l的斜率不存在时，由
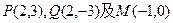知结论也成立，综上，当m =－1时，MP⊥MQ.
（11分）略
练习册系列答案
相关题目
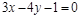被曲线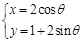
(
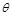为参数)所截得的弦长为_________.
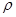cos（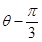
）=1，M,N分别为C与x轴，y轴的交点。
（
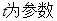）被曲线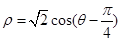
所截的弦长.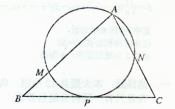
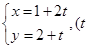为参数），被圆
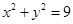截得的弦长为
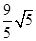
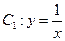绕原点逆时针旋转
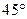后可得到曲线
，
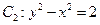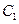变换到曲线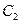
对应的矩阵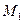
；.
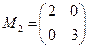，求曲线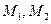
对应的变换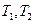
变换后得到的曲线方程.
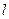的参数方程为
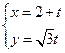（t为参数），曲线C的极坐标方程为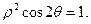
，（
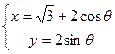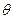为参数），
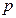是⊙C与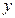
轴正半轴的交点，以圆心C为极点，
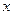轴正半轴为极轴建立极坐标系.
（
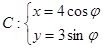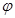为参数）．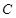
的方程化为普通方程；
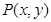是曲线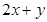
的取值范围．
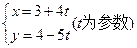的斜率为