题目内容
如图,在四边形ABCD中,已知AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,则BC的长为______.
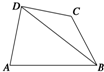

在△ABD中,设BD=x,则BA2=BD2+AD2-2BD•AD•cos∠BDA,即142=x2+102-2•10x•cos60°,
整理得x2-10x-96=0,解之得x1=16,x2=-6(舍去).
在△BCD中,由正弦定理:
=
,
∴BC=
•sin30°=8
.
故答案为:8
整理得x2-10x-96=0,解之得x1=16,x2=-6(舍去).
在△BCD中,由正弦定理:
| BC |
| sin∠CDB |
| BD |
| sin∠BCD |
∴BC=
| 16 |
| sin135° |
| 2 |
故答案为:8
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
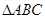 中,角
中,角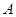 、
、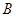 、
、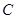 的对边分别为
的对边分别为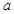 、
、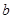 、
、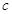 ,且
,且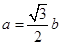 ,
,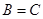 .(1) 求
.(1) 求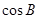 的值;
的值;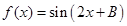 ,求
,求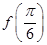 的值.
的值.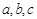 分别为
分别为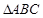 的三个内角
的三个内角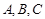 的对边,且
的对边,且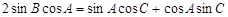 .
.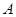 的大小; (2)若
的大小; (2)若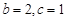 ,
,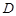 为
为 的中点,求
的中点,求 的长.
的长.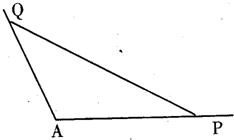
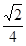
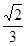
 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是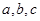 ,已知
,已知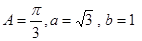 ,则
,则 边等于( )
边等于( )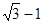
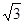
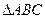 中,角
中,角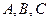 对应的边分别为
对应的边分别为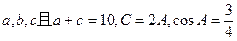
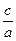 的值 (2)求b的值
的值 (2)求b的值