题目内容
【题目】设满足以下两个条件的有穷数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为 ![]() 阶“期待数列”:
阶“期待数列”:
① ![]() ;
;
② ![]() .
.
(1)分别写出一个单调递增的 3 阶和 4 阶“期待数列”.
(2)若某 2017 阶“期待数列”是等差数列,求该数列的通项公式.
(3)记 ![]() 阶“期待数列”的前
阶“期待数列”的前 ![]() 项和为
项和为 ![]() ,试证:
,试证: ![]() .
.
【答案】
(1)解:三阶: 1 2 , 0 , 1 2 四阶: 3 8 , 1 8 , 1 8 , 3 8 .
(2)解:设等差数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 公差为
公差为 ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,即
,即 ![]() ,
,
∴ ![]() 且
且 ![]() 时与①②矛盾,
时与①②矛盾,![]() 时,由①②得:
时,由①②得: ![]() ,
,
∴ ![]() ,即
,即 ![]() ,
,
由 ![]() 得
得 ![]() ,即
,即 ![]() ,
,
∴ ![]() ,
,
令 ![]() ,
,
∴ ![]() ,
,![]() 时,同理得
时,同理得 ![]() ,
,
即 ![]() ,
,
由 ![]() 得
得 ![]() 即
即 ![]() ,
,
∴ ![]() ,
,
∴ ![]() 时,
时, ![]() .
.
(3)解:当 ![]() 时,显然
时,显然 ![]() 成立;
成立;
当 ![]() 时,根据条件①得
时,根据条件①得 ![]() ,
,![]() ,
,
即 ![]() ,
,![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)弄清新定义n 阶“期待数列”的含义,写出3 阶“期待数列”和4 阶“期待数列”即可;
(2)由2017 阶“期待数列”是等差数列,则要求数列有2017项,且这2017项的和为0,绝对值的和为1,设出数列的公差,对公差d=0,d>0,d<0,分别讨论求出通项;
(3)庑讨论k=n时,由定义得证,再讨论k<n时,由绝对值的性质即可证明不等式.

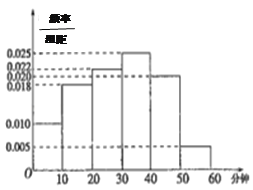
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的2×2列联表,若按95%的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)现在从该地区非体育迷的电视观众中,采用分层抽样方法选取5名观众,求从这5名观众选取两人进行访谈,被抽取的2名观众中至少有一名女生的概率.
附:![]()
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |