题目内容
10.已知函数f(x)=cos2(x-$\frac{π}{6}$)-sin2x,其中x∈R.(1)求函数f(x)的值域;
(2)已知α为第二象限角,且f($\frac{α}{2}$-$\frac{π}{6}$)=$\frac{\sqrt{3}}{3}$,求$\frac{1+cos2α-sin2α}{\sqrt{2}sin(α-\frac{π}{4})}$的值.
分析 (1)利用余弦加法定理、降阶公式、三函数恒等式、二倍角公式推导出f(x)=$\frac{\sqrt{3}}{2}$sin(2x+$\frac{π}{3}$),由此能求出函数f(x)的值域.
(2)由已知$\frac{\sqrt{3}}{2}sinα=\frac{\sqrt{3}}{3}$,从而sinα=$\frac{2}{3}$,cosα=-$\frac{\sqrt{5}}{3}$,进而求出cos2α,sin2α,sin($α-\frac{π}{4}$)的值,由此能求出$\frac{1+cos2α-sin2α}{\sqrt{2}sin(α-\frac{π}{4})}$的值.
解答 解:(1)∵f(x)=cos2(x-$\frac{π}{6}$)-sin2x
=(cosxcos$\frac{π}{6}$+sinxsin$\frac{π}{6}$)2-sin2x
=($\frac{\sqrt{3}}{2}cosx+\frac{1}{2}sinx$)2-sin2x
=$\frac{3}{4}co{s}^{2}x+\frac{1}{4}si{m}^{2}x+\frac{\sqrt{3}}{2}sinxcosx$-sin2x
=$\frac{3}{4}(co{s}^{2}x-si{n}^{2}x)+\frac{\sqrt{3}}{2}sinxcosx$
=$\frac{3}{4}cos2x+\frac{\sqrt{3}}{4}sin2x$
=$\frac{\sqrt{3}}{2}$sin(2x+$\frac{π}{3}$),
∴函数f(x)的值域为[-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$].
(2)∵α为第二象限角,且f($\frac{α}{2}$-$\frac{π}{6}$)=$\frac{\sqrt{3}}{3}$,
∴$\frac{\sqrt{3}}{2}sinα=\frac{\sqrt{3}}{3}$,解得sinα=$\frac{2}{3}$,∴cosα=-$\sqrt{1-(\frac{2}{3})^{2}}$=-$\frac{\sqrt{5}}{3}$,
∴cos2α=1-2sin2α=1-2×$\frac{4}{9}$=$\frac{1}{9}$,sin2α=2sinαcosα=2×$\frac{2}{3}×(-\frac{\sqrt{5}}{3})$=-$\frac{4\sqrt{5}}{9}$,
sin($α-\frac{π}{4}$)=sin$αcos\frac{π}{4}$-cos$αsin\frac{π}{4}$=$\frac{2}{3}×\frac{\sqrt{2}}{2}+\frac{\sqrt{5}}{3}×\frac{\sqrt{2}}{2}=\frac{2\sqrt{2}+\sqrt{10}}{6}$,
∴$\frac{1+cos2α-sin2α}{\sqrt{2}sin(α-\frac{π}{4})}$=$\frac{1+\frac{1}{9}+\frac{4\sqrt{5}}{9}}{\sqrt{2}×\frac{2\sqrt{2}+\sqrt{10}}{6}}$=$\frac{10+4\sqrt{5}}{9}×\frac{3}{2+\sqrt{5}}$=$\frac{2\sqrt{5}}{3}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意余弦加法定理、降阶公式、三函数恒等式、二倍角公式、同角三角函数关系式的合理运用.

| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{21-6\sqrt{3}}$ | D. | 3 |
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 等腰且钝角三角形 | D. | 等腰三角形 |
 如图所示,梯形ABCD中,AB∥CD,AD=BC=5,AB=10,CD=4,动点P自B点出发沿路线BC→CD→DA运动,最后到达A点你的P的运动路程为x,△ABP面积为y,试求y=f(x).
如图所示,梯形ABCD中,AB∥CD,AD=BC=5,AB=10,CD=4,动点P自B点出发沿路线BC→CD→DA运动,最后到达A点你的P的运动路程为x,△ABP面积为y,试求y=f(x).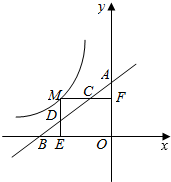 如图,M为曲线y=-$\frac{4}{x}$上的一点.过点M作x轴、y轴的垂线.垂足分别为E、F.分别交直线y=$\frac{\sqrt{3}}{3}$x+m于点D、C两点.若直线y=$\frac{\sqrt{3}}{3}$x+m与y轴交于点A.与x轴相交于点B;
如图,M为曲线y=-$\frac{4}{x}$上的一点.过点M作x轴、y轴的垂线.垂足分别为E、F.分别交直线y=$\frac{\sqrt{3}}{3}$x+m于点D、C两点.若直线y=$\frac{\sqrt{3}}{3}$x+m与y轴交于点A.与x轴相交于点B;