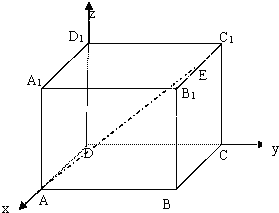
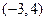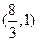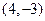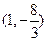题目内容
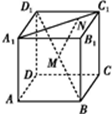
已知长方体ABCD-A1B1C1D1中,DA=DD1=1,DC=
,点E是B1C1的中点,建立空间直角坐标系D-xyz如图所示,则|AE|=______.
| 2 |

由题意长方体ABCD-A1B1C1D1中,DA=DD1=1,DC=
,点E是B1C1的中点,
建立空间直角坐标系D-xyz如图所示,A(1,0,0),E(
,
,1),∴
=(-
,
,1)
∴|
|=
=
;
故答案为:
.
| 2 |
建立空间直角坐标系D-xyz如图所示,A(1,0,0),E(
| 1 |
| 2 |
| 2 |
| AE |
| 1 |
| 2 |
| 2 |
∴|
| AE |
(-
|
| ||
| 2 |
故答案为:
| ||
| 2 |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
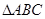 的外接圆圆心为
的外接圆圆心为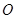 ,半径为2,
,半径为2,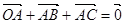 ,且
,且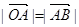 ,向量
,向量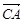 在
在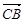 方向上的投影为 ( )
方向上的投影为 ( )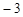
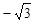
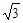
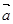 、
、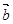 的坐标满足
的坐标满足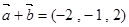 ,
,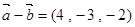 ,则
,则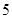
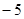
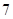
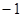
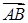 =(2,4,5),
=(2,4,5),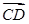 =(3,x,y),若
=(3,x,y),若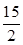
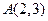 ,
,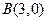 ,且
,且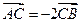 ,则点
,则点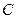 的坐标为 ( )
的坐标为 ( )