题目内容
数列{an}的前n项和为Sn,且满足log2an+1=1+log2an,若S10=10,则a11+a12+…+a20的值等于
- A.10×211
- B.10×210
- C.11×211
- D.11×210
B
分析:由对数的运算性质将log2an+1=1+log2an变形,转化成等比数列,在利用等比数列的前n项和或者利用数列前n项和的性质求解.
解答:∵log2an+1=1+log2an∴log2an+1=log22+log2an=log22an∴an+1=2an
∴数列{an}为公比q=2的正项等比数列
∴S10=10=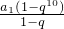 则a11+a12+…+a20=S20-S10=
则a11+a12+…+a20=S20-S10= -
-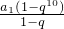 =
=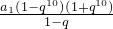 -
-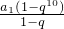
=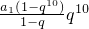 =10×210
=10×210
故选B
点评:本题主要考查对数的运算法则,等比数列的前n项和及运算过程中的整体代换;属于基础知识,常规思路的考查.
分析:由对数的运算性质将log2an+1=1+log2an变形,转化成等比数列,在利用等比数列的前n项和或者利用数列前n项和的性质求解.
解答:∵log2an+1=1+log2an∴log2an+1=log22+log2an=log22an∴an+1=2an
∴数列{an}为公比q=2的正项等比数列
∴S10=10=
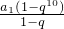 则a11+a12+…+a20=S20-S10=
则a11+a12+…+a20=S20-S10= -
-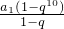 =
=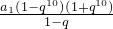 -
-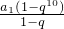
=
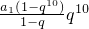 =10×210
=10×210故选B
点评:本题主要考查对数的运算法则,等比数列的前n项和及运算过程中的整体代换;属于基础知识,常规思路的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目