题目内容
已知数列{an}满足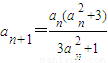 .
.(1)若方程f(x)=x的解称为函数y=f(x)的不动点,求an+1=f(an)的不动点的值;
(2)若a1=2,
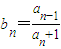 ,求数列{bn}的通项.
,求数列{bn}的通项.(3)当n≥3时,求证:
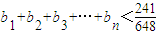 .
.
【答案】分析:(1)利用不动点的定义,根据方程an+1=f(an)得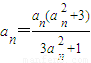 ,由此可得结论;
,由此可得结论;
(2)由数列递推式,写出两式,两式相除,可得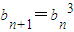 ,由此可得数列{bn}的通项;
,由此可得数列{bn}的通项;
(3)先证明bn=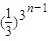 <
<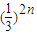 (n≥3),再利用等比数列的求和公式,即可得到结论.
(n≥3),再利用等比数列的求和公式,即可得到结论.
解答:(1)解:由方程an+1=f(an)得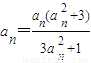 ,解得an=0或an=-1或an=1.…(2分)
,解得an=0或an=-1或an=1.…(2分)
(2)解: =
=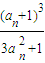 ,
,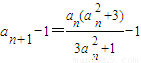 =
=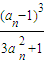
两式相除得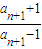 =
=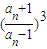 ,即
,即 …(5分)
…(5分)
由a1=2可以得到bn>0,则lnbn+1=3lnbn
又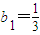 得lnb1=-ln3,
得lnb1=-ln3,
∴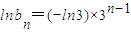 =ln
=ln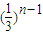
∴bn=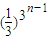 .…(8分)
.…(8分)
(3)证明:当n≥3时,3n-1=(1+2)n-1≥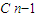 +2
+2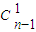 +…+
+…+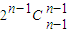 >2n
>2n
∴bn=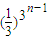 <
<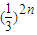 (n≥3)…(11分)
(n≥3)…(11分)
当n≥3时,b1+b2+b3+…+bn<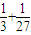 +
+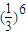 …+
…+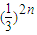 =
=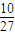 +
+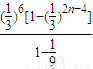 <
<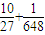 =
=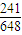 …(14分)
…(14分)
点评:本题考查数列递推式,考查数列的通项,考查不等式的证明,考查学生分析解决问题的能力,考查放缩法的运用,属于中档题.
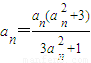 ,由此可得结论;
,由此可得结论;(2)由数列递推式,写出两式,两式相除,可得
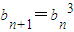 ,由此可得数列{bn}的通项;
,由此可得数列{bn}的通项;(3)先证明bn=
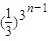 <
<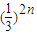 (n≥3),再利用等比数列的求和公式,即可得到结论.
(n≥3),再利用等比数列的求和公式,即可得到结论.解答:(1)解:由方程an+1=f(an)得
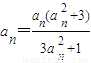 ,解得an=0或an=-1或an=1.…(2分)
,解得an=0或an=-1或an=1.…(2分)(2)解:
 =
=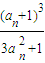 ,
,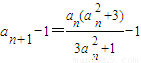 =
=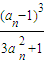
两式相除得
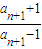 =
=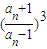 ,即
,即 …(5分)
…(5分)由a1=2可以得到bn>0,则lnbn+1=3lnbn
又
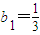 得lnb1=-ln3,
得lnb1=-ln3,∴
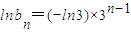 =ln
=ln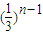
∴bn=
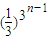 .…(8分)
.…(8分)(3)证明:当n≥3时,3n-1=(1+2)n-1≥
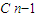 +2
+2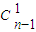 +…+
+…+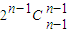 >2n
>2n∴bn=
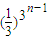 <
<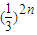 (n≥3)…(11分)
(n≥3)…(11分)当n≥3时,b1+b2+b3+…+bn<
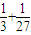 +
+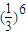 …+
…+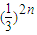 =
=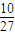 +
+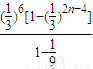 <
<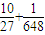 =
=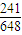 …(14分)
…(14分)点评:本题考查数列递推式,考查数列的通项,考查不等式的证明,考查学生分析解决问题的能力,考查放缩法的运用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目