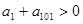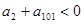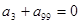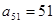题目内容
已知数列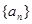 满足
满足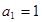 ,且
,且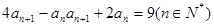 .
.
⑴求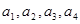 的值;
的值;
⑵猜想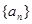 的通项公式,请证明你的猜想.
的通项公式,请证明你的猜想.
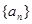 满足
满足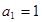 ,且
,且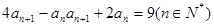 .
.⑴求
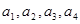 的值;
的值;⑵猜想
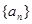 的通项公式,请证明你的猜想.
的通项公式,请证明你的猜想.⑴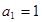
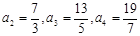
⑵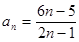
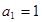
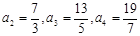
⑵
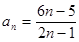
(1)代入已知式子求出数列的前4项;(2)根据前4项归纳出数列的通项,然后按照数学归纳法的步骤证明通项式子成立
解:
⑴由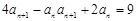 得
得 ,求得
,求得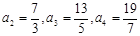 .
.
⑵ 猜想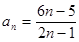
证明:①当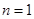 时,猜想成立。
时,猜想成立。
②设当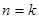 时
时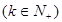 时,猜想成立,即
时,猜想成立,即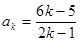 ,则当
,则当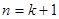 时,
时,
有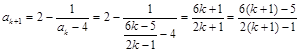 ,所以当
,所以当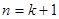 时猜想也成立,③综合①②,猜想对任何
时猜想也成立,③综合①②,猜想对任何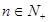 都成立.
都成立.
解:
⑴由
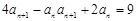 得
得 ,求得
,求得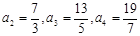 .
.⑵ 猜想
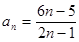
证明:①当
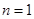 时,猜想成立。
时,猜想成立。②设当
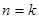 时
时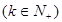 时,猜想成立,即
时,猜想成立,即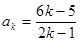 ,则当
,则当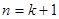 时,
时,有
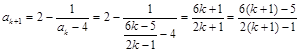 ,所以当
,所以当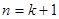 时猜想也成立,③综合①②,猜想对任何
时猜想也成立,③综合①②,猜想对任何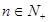 都成立.
都成立.
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
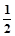 ,且前n项和Sn满足:Sn=n2an,求a2,a3,a4,猜想{an}的通项公式,并加以证明。
,且前n项和Sn满足:Sn=n2an,求a2,a3,a4,猜想{an}的通项公式,并加以证明。 中,已知
中,已知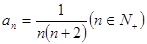 ,则
,则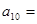 ▲ .
▲ . 为
为
 的各位数字之和,如
的各位数字之和,如 ,
, ,则
,则 ;记
;记 ,
, ,…,
,…, ,
, ,则
,则 = .
= . 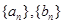 的前n项和分别为
的前n项和分别为 和
和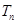 ,若
,若 ,且
,且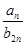 是整数,则
是整数,则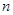 的值为 ;
的值为 ;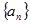 中,
中, 是其前
是其前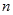 项和,
项和,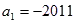 ,
,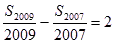 ,则
,则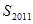 的值为( )
的值为( )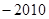

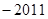
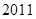
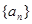 的前
的前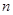 项和为
项和为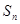 ,且
,且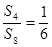 ,则
,则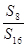 =( )
=( )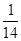
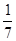
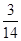
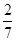
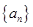 的前
的前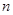 项和为
项和为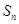 ,若
,若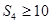 ,
,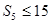 ,则
,则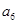 的最大值为 .
的最大值为 .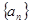 满足
满足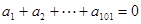 ,则 ( )
,则 ( )