Question

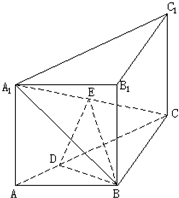（2005•朝阳区一模）直三棱柱ABC-A₁B₁C₁中，AB⊥BC，E是A₁C的中点，ED⊥A₁C且交AC于D，A1A=AB=

2

2

BC．
（I）证明：B₁C₁∥平面A₁BC；
（II）证明：A₁C⊥平面EDB；
（III）求平面A₁AB与平面EDB所成的二面角的大小（仅考虑平面角为锐角的情况）．

Answer 1

分析：（I）根据三棱柱的几何特征，可得B₁C₁∥BC，进而根据线面平行的判定定理得到B₁C₁∥平面A₁BC；
（II）根据直三棱柱的几何特征，又由BC=A₁B，E是等腰△A₁BC底边A₁C的中点，可得A₁C⊥BE，结合线面垂直的判定定理可得A₁C⊥平面EDB；
（III）设交点为E，连接EF，可确定出∠A₁BE是所求的二面角的平面角，解A₁BE可得平面A₁AB与平面EDB所成的二面角的大小．

解答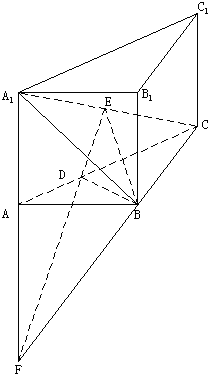：证明：（I）∵三棱柱ABC-A₁B₁C₁中B₁C₁∥BC，（1分）
又BC?平面A₁BC，且B₁C₁?平面A₁BC，
∴B₁C₁∥平面A₁BC（3分）
（II）∵三棱柱ABC-A₁B₁C₁中A₁A⊥AB，
∴Rt△A₁AB中AB=

2

2

A1B又A1A=AB=

2

2

BC
∴BC=A₁B，
∴△A₁BC是等腰三角形（6分）
∵E是等腰△A₁BC底边A₁C的中点，
∴A₁C⊥BE①
又依条件知A₁C⊥ED②
且ED∩BE=E③
由①，②，③得A₁C⊥平面EDB（8分）
解：（III）∵A₁A、ED?平面A₁AC，
且A₁A、ED不平行，
故延长A₁A，ED后必相交，
设交点为F，连接EF，如图
∴A₁-BF-E是所求的二面角（10分）
依条件易证明Rt△A₁EF≌Rt△A₁AC∵E为A₁C中点，
∴A为A₁F中点∴AF=A₁A=AB
∴∠A₁BA=∠ABF=45°
∴∠A₁FB=90°
即A₁B⊥FB（12分）
又A₁E⊥平面EFB，
∴EB⊥FB
∴∠A₁BE是所求的二面角的平面角（13分）
∵E为等腰直角三角形A₁BC底边中点，
∴∠A₁BE=45°
故所求的二面角的大小为45°（14分）

点评：本题考查的知识点是与二面角有关的立体几何综合题，直线与平面平行的判定，直线与平面垂直的判定，熟练掌握线面关系的判定定理及二面角平面角的确定方法是解答本题的关键．