题目内容
设a为实数,函数f(x)=x3+ax2+(a-3)x的导函数为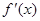 ,且
,且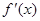 是偶函数, 则曲线:y=f(x)在点(2,f(2))处的切线方程为 .
是偶函数, 则曲线:y=f(x)在点(2,f(2))处的切线方程为 .
9x—y—16 = 0
解析试题分析: ,因为
,因为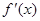 是偶函数,所以
是偶函数,所以 ,解得a=0,所以
,解得a=0,所以
切线的斜率k= =9,f(2)=23-3×2=2,所求切线方程为y-2=9(x-2),即9x—y—16 = 0.
=9,f(2)=23-3×2=2,所求切线方程为y-2=9(x-2),即9x—y—16 = 0.
考点:1.函数的导数;2.函数的奇偶性;3.导数的几何意义.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
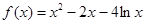 ,则
,则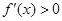 的解集为 。
的解集为 。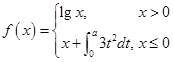 ,
,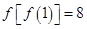 ,则
,则 的值为__________.
的值为__________.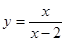 在点(1,-1)处的切线方程为 .
在点(1,-1)处的切线方程为 . 在区间
在区间 上的零点的近似值(精确度
上的零点的近似值(精确度 )是 .
)是 . 





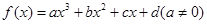 的对称中心为
的对称中心为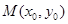 ,记函数
,记函数 的导函数为
的导函数为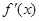 ,
,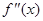 ,则有
,则有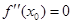 .若函数
.若函数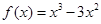 ,则可求得
,则可求得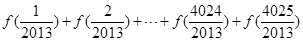 _________.
_________. 在点
在点 处的切线方程为 ___________________
处的切线方程为 ___________________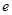 是自然对数的底数,若函数
是自然对数的底数,若函数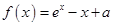 的图象始终在
的图象始终在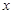 轴的上方,则实数
轴的上方,则实数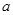 的取值范围 .
的取值范围 .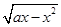 (a>0)的单调递减区间是________.
(a>0)的单调递减区间是________.