题目内容
1．设θ的终边过点P（-4，3），那么3sinθ+cosθ=1．分析 由条件利用任意角的三角函数的定义，求得sinθ和cosθ 的值，可得3sinθ+cosθ的值．
解答 解：∵θ的终边过点P（-4，3），
则x=-4，y=3，r=|OP|=5．
∴sinθ=$\frac{y}{r}=\frac{3}{5}$，cosθ=$\frac{x}{r}=-\frac{4}{5}$．
则3sinθ+cosθ=3×$\frac{3}{5}$+（-$\frac{4}{5}$）=1．
故答案为：1．
点评 本题主要考查任意角的三角函数的定义，属于基础题．
练习册系列答案
相关题目
11．直线y=kx+1（k∈R）与椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1恒有公共点，则实数m的取值范围为（ ）
| A． | （0，1） | B． | （0，5） | C． | [1，5）∪（5，+∞） | D． | （1+∞） |
9．小明要给刚结识的朋友小林打电话，他只记住了电话号码8个数字的前面5个数字的顺序，后3个数字是3、6、8三个数字的某一种排列顺序，但具体顺序忘记了，那么小明第一次就拨通电话的概率是（ ）
| A． | $\frac{1}{12}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{3}$ |
16．若α∈（0，2π），且tanα＞cotα＞cosα＞sinα，则α的取值范围是（ ）
| A． | （$\frac{π}{4}$，$\frac{π}{2}$） | B． | （$\frac{3π}{4}$，π） | C． | （$\frac{5π}{4}$，$\frac{3π}{2}$） | D． | （$\frac{7π}{4}$，2π） |
6．某园林局对1 000株树木的生长情况进行调查，其中杉树600株，槐树400株．现用分层抽样方法从这1 000株树木中随机抽取100株，杉树与槐树的树干周长（单位：cm）的抽查结果如表：
（1）求x，y值；
（2）树干周长在30cm到40cm之间的4株槐树有1株患虫害，现要对这4株树逐一进行排查直至找出患虫害的树木为止，求排查的树木恰好为2株的概率．
| 树干周长（单位：cm） | [30，40） | [40，50） | [50，60） | [60，70） |
| 杉树 | 6 | 19 | 21 | x |
| 槐树 | 4 | 20 | y | 6 |
（2）树干周长在30cm到40cm之间的4株槐树有1株患虫害，现要对这4株树逐一进行排查直至找出患虫害的树木为止，求排查的树木恰好为2株的概率．
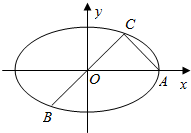如图所示，已知A、B、C是长轴为4的椭圆E上的三点，点A是长轴的一个端点，BC过椭圆中心O，且AC⊥BC，|BC|=2|AC|．