题目内容
直线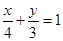 与椭圆
与椭圆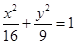 相交于
相交于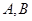 两点,该椭圆上点
两点,该椭圆上点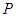 使
使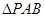 的面积等于6,这样的点
的面积等于6,这样的点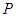 共有( )
共有( )
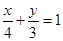 与椭圆
与椭圆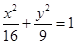 相交于
相交于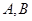 两点,该椭圆上点
两点,该椭圆上点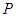 使
使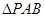 的面积等于6,这样的点
的面积等于6,这样的点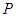 共有( )
共有( )| A.1个 | B.2个 | C.3个 | D.4个 |
B
试题分析:直线
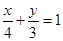 与
与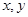 的交点分别为
的交点分别为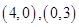 ,恰好为椭圆的一个长轴端点和一个短轴端点,所以这两个点即为直线
,恰好为椭圆的一个长轴端点和一个短轴端点,所以这两个点即为直线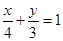 与椭圆
与椭圆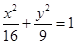 的交点,所以
的交点,所以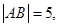 因为
因为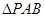 的面积等于6,所以点
的面积等于6,所以点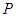 到直线
到直线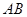 的距离为
的距离为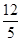 ,下面问题就转化为与直线
,下面问题就转化为与直线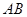 平行且距离为
平行且距离为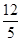 的直线与椭圆有几个交点.可以设与
的直线与椭圆有几个交点.可以设与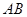 平行的直线为
平行的直线为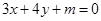 ,利用平行线间的距离公式可以求得
,利用平行线间的距离公式可以求得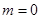 或
或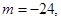 当
当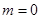 时,直线过椭圆中心,所以和椭圆有两个交点,当
时,直线过椭圆中心,所以和椭圆有两个交点,当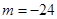 时,直线与椭圆相离,所以只有两个符合条件的点
时,直线与椭圆相离,所以只有两个符合条件的点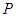 .
.点评:比较复杂的问题要合理转化,比如本题最后就转化成了直线与椭圆的交点各数问题,这样才能化繁为简,使问题得到解决.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
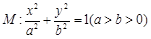 的离心率为
的离心率为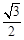 ,直线
,直线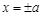 和
和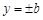 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.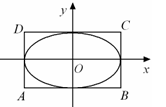
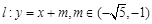 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点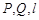 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点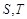 .求
.求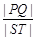 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值. 的离心率
的离心率 ,其中一个顶点坐标为
,其中一个顶点坐标为 ,则椭圆的方程为 .
,则椭圆的方程为 .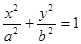 (a>
(a>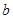 )中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角
)中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角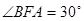 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



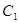 的离心率为
的离心率为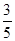 ,焦点在
,焦点在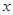 轴上,且长轴长为10,曲线
轴上,且长轴长为10,曲线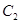 上的点与椭圆
上的点与椭圆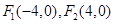 ,动点
,动点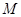 满足条件:
满足条件: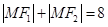 ,则点
,则点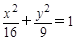
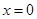
 (
(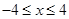 )
)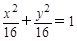
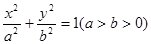 的左、右焦点,A和B是以O(O为坐标原点)为圆心,以|OF1|为半径的圆与该椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )
的左、右焦点,A和B是以O(O为坐标原点)为圆心,以|OF1|为半径的圆与该椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )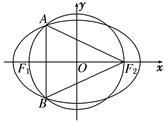


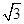 -1
-1 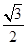
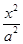 +
+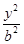 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,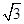 ,
,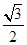 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.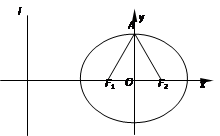
 轴,短轴所在直线为
轴,短轴所在直线为 轴,建立平面直角坐标系,如图所示:
轴,建立平面直角坐标系,如图所示: