题目内容
已知直三棱柱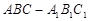 中,△
中,△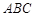 为等腰直角三角形,∠
为等腰直角三角形,∠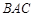 =90°,且
=90°,且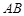 =
=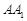 ,
,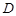 、
、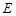 、
、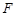 分别为
分别为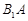 、
、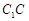 、
、 的中点.
的中点.
(1)求证: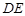 ∥平面
∥平面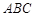 ;
;
(2)求证: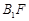 ⊥平面
⊥平面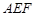 ;
;
(3)求二面角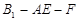 的余弦值
的余弦值
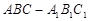 中,△
中,△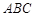 为等腰直角三角形,∠
为等腰直角三角形,∠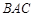 =90°,且
=90°,且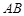 =
=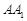 ,
,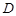 、
、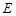 、
、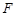 分别为
分别为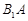 、
、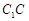 、
、 的中点.
的中点.
(1)求证:
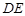 ∥平面
∥平面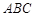 ;
;(2)求证:
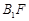 ⊥平面
⊥平面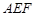 ;
;(3)求二面角
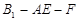 的余弦值
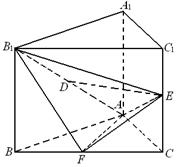
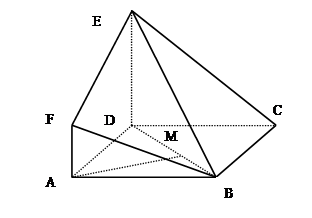
的余弦值解:如图建立空间直角坐标系O—xyz,令AB=AA1=4,

则A(0,0,0),E(0,4,2),F(2,2,0),B(4,0,0),
B1(4,0,4),D(2,0,2), …………(2分)
(1) (
(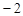 ,4,0),面ABC的法向量为
,4,0),面ABC的法向量为 (0,0,4),
(0,0,4),
∵
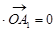 ,
, 平面ABC,
平面ABC,
∴DE∥平面ABC. …………(4分)
(2)
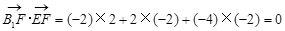
 …………(6分)
…………(6分)
∴
∵ …………(8分)
…………(8分)
(3) 平面AEF的法向量为
 ,设平面 B1AE的法向量为
,设平面 B1AE的法向量为
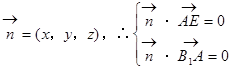 即
即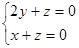 …………(10分)
…………(10分)
令x=2,则
∴
∴二面角B1—AE—F的余弦值为


则A(0,0,0),E(0,4,2),F(2,2,0),B(4,0,0),
B1(4,0,4),D(2,0,2), …………(2分)
(1)
 (
(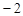 ,4,0),面ABC的法向量为
,4,0),面ABC的法向量为 (0,0,4),
(0,0,4),∵

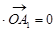 ,
, 平面ABC,
平面ABC,∴DE∥平面ABC. …………(4分)
(2)

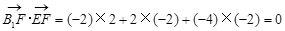
 …………(6分)
…………(6分)∴

∵
 …………(8分)
…………(8分)(3) 平面AEF的法向量为

 ,设平面 B1AE的法向量为
,设平面 B1AE的法向量为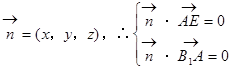 即
即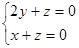 …………(10分)
…………(10分)令x=2,则

∴

∴二面角B1—AE—F的余弦值为


略

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 是边长为3的正方形,
是边长为3的正方形,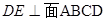 ,
, ,
,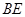 与平面
与平面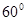 .
.
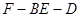 的的余弦值;
的的余弦值;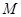 是线段
是线段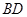 上一动点,试确定
上一动点,试确定 ,并证明你的结论.
,并证明你的结论.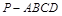 的底面
的底面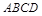 是正方形,侧棱
是正方形,侧棱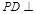 底面
底面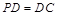 ,
,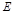 是
是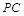 的中点.
的中点.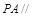 平面
平面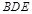 ;
;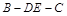 的余弦值.
的余弦值.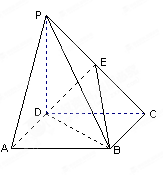
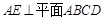 ,
, ,
,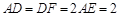 .
.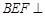 平面
平面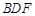 ;
;
 中,底面
中,底面 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱 面
面 是
是 的中点.
的中点. ;(2)求证:
;(2)求证: ∥平面
∥平面

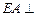 平面
平面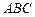 ,
,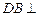 平面
平面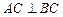 ,
,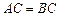
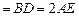 ,
,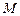 是
是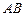 的中点.建立适当的空间直角坐标系,解决下列问题:
的中点.建立适当的空间直角坐标系,解决下列问题: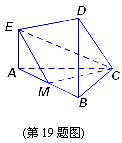
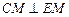 ;
;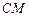 与平面
与平面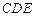 所成角的大小.
所成角的大小.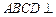 平面
平面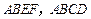 是正方形,
是正方形,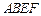 是矩形,且
是矩形,且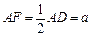 ,
,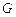 是
是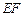 的中点.
的中点.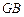 与平面
与平面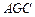 所成角
所成角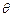 的正弦值;
的正弦值;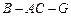 的余弦值.
的余弦值.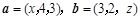 ,且
,且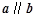 ,则
,则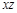 等于( )
等于( )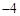
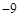
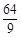
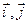 分别是
分别是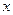 轴,
轴,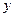 轴正方向上的单位向量,
轴正方向上的单位向量,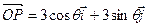 ,
,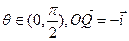 。若用?来表示
。若用?来表示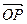 与
与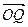 的夹角,则?等于 ( )
的夹角,则?等于 ( )