题目内容
.已知圆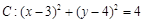 ,直线
,直线 过定点 A (1,0).
过定点 A (1,0).
(1)若 与圆C相切,求
与圆C相切,求 的方程;
的方程;
(2)若 的倾斜角为
的倾斜角为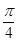 ,
, 与圆C相交于P,Q两点,求线段PQ的中点M的坐标;
与圆C相交于P,Q两点,求线段PQ的中点M的坐标;
(3)若 与圆C相交于P,Q两点,求△CPQ面积的最大值
与圆C相交于P,Q两点,求△CPQ面积的最大值
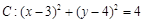 ,直线
,直线 过定点 A (1,0).
过定点 A (1,0).(1)若
 与圆C相切,求
与圆C相切,求 的方程;
的方程; (2)若
 的倾斜角为
的倾斜角为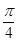 ,
, 与圆C相交于P,Q两点,求线段PQ的中点M的坐标;
与圆C相交于P,Q两点,求线段PQ的中点M的坐标;(3)若
 与圆C相交于P,Q两点,求△CPQ面积的最大值
与圆C相交于P,Q两点,求△CPQ面积的最大值解:①若直线 的斜率不存在,则直线
的斜率不存在,则直线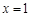 ,符合题意.……………… 1分
,符合题意.……………… 1分
②若直线 的斜率存在,设直线
的斜率存在,设直线 为
为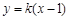 ,即
,即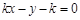 ………… 2分
………… 2分
由题意知,圆心(3,4)到直线 的距离等于半径2,即:
的距离等于半径2,即: 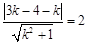 …… 3分
…… 3分
解之得 …………………………………………………4分
…………………………………………………4分
所求直线 方程是
方程是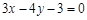 ……………………………………………5分
……………………………………………5分
综上所述:所求直线 方程是
方程是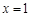 ,或
,或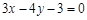 ………………………6分
………………………6分
(2) 直线 的方程为y= x-1………………………………………………………………………7分
的方程为y= x-1………………………………………………………………………7分
∵M是弦PQ的中点,∴PQ⊥CM,
∴CM方程为y-4=-(x-3),即x+y-7=0……………………………………8分
∵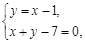 …………………………………………9分
…………………………………………9分
∴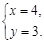 …………………………………………10分
…………………………………………10分
∴M点坐标(4,3).……………………………………………………………………………11分
(3)设圆心到直线的距离为d,三角形CPQ的面积为S,则…………12分
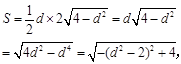 ………………………………………14分
………………………………………14分
∴当d=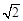 时,S取得最大值2. ………………16分
时,S取得最大值2. ………………16分
 的斜率不存在,则直线
的斜率不存在,则直线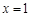 ,符合题意.……………… 1分
,符合题意.……………… 1分②若直线
 的斜率存在,设直线
的斜率存在,设直线 为
为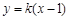 ,即
,即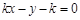 ………… 2分
………… 2分由题意知,圆心(3,4)到直线
 的距离等于半径2,即:
的距离等于半径2,即: 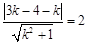 …… 3分
…… 3分解之得
 …………………………………………………4分
…………………………………………………4分所求直线
 方程是
方程是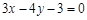 ……………………………………………5分
……………………………………………5分综上所述:所求直线
 方程是
方程是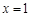 ,或
,或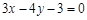 ………………………6分
………………………6分(2) 直线
 的方程为y= x-1………………………………………………………………………7分
的方程为y= x-1………………………………………………………………………7分∵M是弦PQ的中点,∴PQ⊥CM,
∴CM方程为y-4=-(x-3),即x+y-7=0……………………………………8分
∵
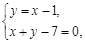 …………………………………………9分
…………………………………………9分∴
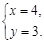 …………………………………………10分
…………………………………………10分∴M点坐标(4,3).……………………………………………………………………………11分
(3)设圆心到直线的距离为d,三角形CPQ的面积为S,则…………12分
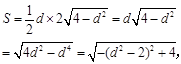 ………………………………………14分
………………………………………14分∴当d=
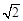 时,S取得最大值2. ………………16分
时,S取得最大值2. ………………16分略

练习册系列答案
相关题目
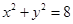 内有一点
内有一点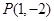 ,
,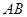 为过点
为过点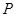 且倾斜角为
且倾斜角为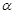 的弦,
的弦,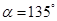 时,求弦
时,求弦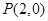 及圆
及圆 :
: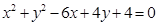 .
.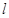 过点
过点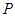 且与圆心
且与圆心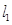 与圆
与圆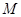 、
、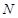 两点,当
两点,当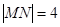 时,求以线段
时,求以线段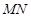 为直径的圆
为直径的圆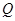 的方程;
的方程;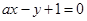 与圆
与圆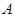 ,
,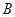 两点,是否存在实数
两点,是否存在实数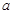 ,使得过点
,使得过点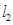 垂直平分弦
垂直平分弦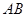 ?若存在,求出实数
?若存在,求出实数 的直线被圆
的直线被圆 所截得的弦长为
所截得的弦长为



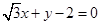 截圆
截圆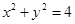 得到的弦长为
得到的弦长为

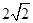
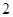
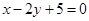 与圆
与圆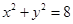 相交于A、B两点,则
相交于A、B两点,则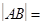 ▲ .
▲ . 直线
直线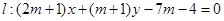 ,
, 恒过的定点;
恒过的定点;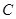 截得的弦长何时最长,何时最短?并求截得的弦长最短时,求
截得的弦长何时最长,何时最短?并求截得的弦长最短时,求 的值以及最短长度。
的值以及最短长度。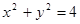 和圆外一点
和圆外一点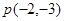 ,求过点
,求过点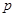 的圆的切线方程。(10分)
的圆的切线方程。(10分)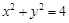 上,与直线4x+3y-12=0的距离最小的点的坐标 .
上,与直线4x+3y-12=0的距离最小的点的坐标 .