题目内容
选做题（考生只能从A、B、C题中选作一题）A、（不等式证明选讲）不等式|x-1|＜|x|+1的解集为
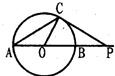
B、（几何证明选讲）已知Rt△ABC的直角边BC的长为3cm，以A为圆心直角边AC为半径的圆交BA于D点，当BD=1cm时，AC长为
C、（坐标系与参数方程）曲线
（θ为参数）到直线x-3y+1=0距离为1.5的点有 个．
【答案】分析：A、由绝对值的意义，得到绝对值不等式的解集，B、由勾股定理解方程求出AC的值；
C、把参数方程化为普通方程后，可得曲线表示圆，圆心在直线上，从而得到圆上到直线x-3y+1=0 的距离等于1.5的点的个数．
解答：解：A、不等式|x-1|＜|x|+1，即|x-1|-|x|＜1，即数轴上的x到1的距离减去到0的距离小于1，故解集为
（0，+∞）．
B、设AC=x，由勾股定理得 9+x2=（x+1）2，∴x=1，即 AC=1．
C、曲线
（θ为参数） 即 （x-2）2+（y-1）2=9，表示以（2，1）为圆心，以3为半径的圆，
圆心到直线x-3y+1=0 的距离为 0，故圆上到直线x-3y+1=0 的距离等于1.5的点共有4个．
故答案为：（0，+∞）、1、4．
点评：本题考查绝对值不等式的解法，圆的参数方程与普通方程的互化．
C、把参数方程化为普通方程后，可得曲线表示圆，圆心在直线上，从而得到圆上到直线x-3y+1=0 的距离等于1.5的点的个数．
解答：解：A、不等式|x-1|＜|x|+1，即|x-1|-|x|＜1，即数轴上的x到1的距离减去到0的距离小于1，故解集为
（0，+∞）．
B、设AC=x，由勾股定理得 9+x2=（x+1）2，∴x=1，即 AC=1．
C、曲线
（θ为参数） 即 （x-2）2+（y-1）2=9，表示以（2，1）为圆心，以3为半径的圆，圆心到直线x-3y+1=0 的距离为 0，故圆上到直线x-3y+1=0 的距离等于1.5的点共有4个．
故答案为：（0，+∞）、1、4．
点评：本题考查绝对值不等式的解法，圆的参数方程与普通方程的互化．
练习册系列答案
相关题目
选做题（考生只能从A、B、C题中选作一题）
选做题（考生只能从A，B，C中选做一题，多做以所做第一题记分）