题目内容
选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)A.(不等式选做题)
已知a∈R,若关于x的方程x2+4x+|a-1|+|a+1|=0无实根,则a的取值范围是 .
B.(几何证明选做题)
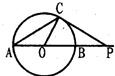
如图,CD是圆O的切线,切点为C,点A、B在圆O上,BC=1,∠BCD=30°,则圆O的面积为 .
C.(坐标系与参数方程选做题)
在极坐标系中,若过点(1,0)且与极轴垂直的直线交曲线ρ=4cosθ于A、B两点,则|AB|= .

【答案】分析:A.一元二次方程无实数根的充要条件是△<0,转化为|a-1|+|a+1|>4,对a分a>1、-1≤a≤1、a<-1三种情况讨论即可;
B.利用弦切角定理和正弦定理即可得出;
C.先把曲线的极坐标方程化为普通方程,再与直线的方程联立解出点A、B的坐标,利用两点间的距离公式即可求出.
解答:解:A.∵关于x的方程x2+4x+|a-1|+|a+1|=0无实根,∴△=42-4(|a-1|+|a+1|)<0,解得|a-1|+|a+1|>4,
①当a>1时,上述不等式可化为2a>4,解得a>2>1,满足条件;
②当-1≤a≤1时,上述不等式可化为2>4,此时不符合条件,应舍去;
③当a<-1时,上述不等式可化为-2a>4,解得a<-2,满足条件.
综上可知:a的取值范围是(-∞,-2)∪(2,+∞).
B.由弦切角定理可得:∠CAB=∠DCB=30°,
在△ABC中,由正弦定理得: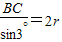 ,r为△ABC的外接圆的半径.
,r为△ABC的外接圆的半径.
∴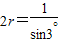 =2,解得r=1,
=2,解得r=1,
∴圆O的面积=π×12=π.
故答案为π.
C.∵曲线ρ=4cosθ,∴ρ2=4ρcosθ,化为普通方程:x2+y2=4x,与直线x=1联立得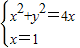 ,解得
,解得 .
.
∴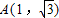 ,
,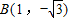 .
.
∴|AB|=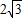 .
.
故答案为 .
.
点评:正确理解一元二次方程无实数根的条件、利用分类讨论方法解含绝对值不等式、弦切角定理和正弦定理、联立方程组的解与曲线与直线的交点、两点间的距离公式是解题的关键.
B.利用弦切角定理和正弦定理即可得出;
C.先把曲线的极坐标方程化为普通方程,再与直线的方程联立解出点A、B的坐标,利用两点间的距离公式即可求出.
解答:解:A.∵关于x的方程x2+4x+|a-1|+|a+1|=0无实根,∴△=42-4(|a-1|+|a+1|)<0,解得|a-1|+|a+1|>4,
①当a>1时,上述不等式可化为2a>4,解得a>2>1,满足条件;
②当-1≤a≤1时,上述不等式可化为2>4,此时不符合条件,应舍去;
③当a<-1时,上述不等式可化为-2a>4,解得a<-2,满足条件.
综上可知:a的取值范围是(-∞,-2)∪(2,+∞).
B.由弦切角定理可得:∠CAB=∠DCB=30°,
在△ABC中,由正弦定理得:
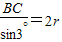 ,r为△ABC的外接圆的半径.
,r为△ABC的外接圆的半径.∴
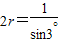 =2,解得r=1,
=2,解得r=1,∴圆O的面积=π×12=π.
故答案为π.
C.∵曲线ρ=4cosθ,∴ρ2=4ρcosθ,化为普通方程:x2+y2=4x,与直线x=1联立得
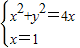 ,解得
,解得 .
.∴
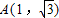 ,
,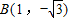 .
.∴|AB|=
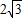 .
.故答案为
 .
.点评:正确理解一元二次方程无实数根的条件、利用分类讨论方法解含绝对值不等式、弦切角定理和正弦定理、联立方程组的解与曲线与直线的交点、两点间的距离公式是解题的关键.

练习册系列答案
相关题目
 选做题(考生只能从A、B、C题中选作一题)
选做题(考生只能从A、B、C题中选作一题) 选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分) (θ为参数)到直线x-3y+1=0距离为1.5的点有 个.
(θ为参数)到直线x-3y+1=0距离为1.5的点有 个.