题目内容
 选做题(考生只能从A、B、C题中选作一题)
选做题(考生只能从A、B、C题中选作一题)A、已知直线x+2y-4=0与
|
B、若关于x的方程x2+4x+|a-1|+|a+1|=0有实根,则实数a的取值范围为
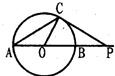
C、如图,⊙O的直径AB=6cm,P是延长线上的一点,过点P作⊙O的切线,切点为C,连接AC,若∠CAP=30°,
则PC=
分析:A、把圆的参数方程化为普通方程后,联立直线和圆的方程,消去x得到关于y的一元二次方程,设出两交点的坐标,把两点坐标代入直线方程即可得到横坐标之差的平方与纵坐标之差的平方的关系,由韦达定理求出纵坐标之差的平方,然后利用两点间的距离公式即可求出|AB|的长;
B、由关于x的方程有实根得到根的判别式大于等于0,列出关于a的不等式,利用数轴上两点间的距离公式,画出数轴即可得到a的取值范围;
C、连接OC,得到OC垂直于PC,因为OA等于OC,利用等边对等角得到角PAC等于角ACO,利用三角形AOC的外角性质可知角COP等于60°,即可得到角P等于30°,由圆的直径等于6cm可得半径OC等于3cm,根据30°角所对的直角边等于斜边的一半及勾股定理即可求出PC的长.
三道题选作一题即可.
B、由关于x的方程有实根得到根的判别式大于等于0,列出关于a的不等式,利用数轴上两点间的距离公式,画出数轴即可得到a的取值范围;
C、连接OC,得到OC垂直于PC,因为OA等于OC,利用等边对等角得到角PAC等于角ACO,利用三角形AOC的外角性质可知角COP等于60°,即可得到角P等于30°,由圆的直径等于6cm可得半径OC等于3cm,根据30°角所对的直角边等于斜边的一半及勾股定理即可求出PC的长.
三道题选作一题即可.
解答:解:A、把圆的方程化为普通方程得:(x-2)2+(y-1)2=9,
联立直线与圆的方程得
,消去x得到:5y2-10y-4=0
设直线与圆的两交点坐标分别为A(x1,y1),B(x2,y2),
而y1+y2=2,y1y2=-
,所以(y1-y2)2=(y1+y2)2-4y1y2=
,
把两点代入直线方程得(x1-x2)2=4(y1-y2)2,
所以|AB|=
=
=6;
B、由题意可知△=16-4(|a-1|+|a+1|)≥0,
即|a-1|+|a+1|≤4,表示数轴上一点a到1和-1的距离之和小于4,画出数轴如下:
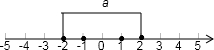
所以a∈[-2,2];
C、连接OC,则OC⊥PC,
∵OA=OC,∴∠CAP=∠ACO=30°,
则∠COP=∠CAP+∠ACO=2∠CAP=60°,所以∠P=30°,
∵AB=6cm,∴OC=3cm,则OP=6cm,
所以PC=
=3
cm.
故答案为:A:6;B:[-2,2];C:3
.
三道题选作一题即可.
联立直线与圆的方程得
|
设直线与圆的两交点坐标分别为A(x1,y1),B(x2,y2),
而y1+y2=2,y1y2=-
| 4 |
| 5 |
| 36 |
| 5 |
把两点代入直线方程得(x1-x2)2=4(y1-y2)2,
所以|AB|=
| (x1-x2) 2+(y1-y2) 2 |
| 5(y1-y2)2 |
B、由题意可知△=16-4(|a-1|+|a+1|)≥0,
即|a-1|+|a+1|≤4,表示数轴上一点a到1和-1的距离之和小于4,画出数轴如下:

所以a∈[-2,2];
C、连接OC,则OC⊥PC,
∵OA=OC,∴∠CAP=∠ACO=30°,
则∠COP=∠CAP+∠ACO=2∠CAP=60°,所以∠P=30°,
∵AB=6cm,∴OC=3cm,则OP=6cm,
所以PC=
| 62-32 |
| 3 |
故答案为:A:6;B:[-2,2];C:3
| 3 |
三道题选作一题即可.
点评:此题要求学生掌握直线与圆的位置关系,灵活运用韦达定理及两点间的距离公式化简求值,利用数形结合的数学思想解决实际问题,掌握圆及直角三角形的基本性质,是一道多知识的综合题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
 (θ为参数)到直线x-3y+1=0距离为1.5的点有 个.
(θ为参数)到直线x-3y+1=0距离为1.5的点有 个.