题目内容
【题目】已知点F1、F2为双曲线![]() (b>0)的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,且∠MF1F2=30°,圆O的方程是x2+y2=b2.
(b>0)的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,且∠MF1F2=30°,圆O的方程是x2+y2=b2.
(1)求双曲线C的方程;
(2)过双曲线C上任意一点P作该双曲线两条渐近线的垂线,垂足分别为P1、P2,求![]() 的值;
的值;
(3)过圆O上任意一点Q作圆O的切线l交双曲线C于A、B两点,AB中点为M,求证:|AB|=2|OM|.
【答案】(1)![]() ;(2)-
;(2)-![]() ;(3)见解析
;(3)见解析
【解析】
(1)解:设F2,M的坐标分别为![]() ,再通过双曲线的定义和解三角形得到双曲线C的方程为
,再通过双曲线的定义和解三角形得到双曲线C的方程为![]() ;(2)设双曲线C上的点P(x0,y0),设两渐近线的夹角为θ,再求出
;(2)设双曲线C上的点P(x0,y0),设两渐近线的夹角为θ,再求出![]() 和
和![]() 的值,即得
的值,即得![]() 的值;(3)由题意,即证:OA⊥OB,分y0≠0和y0=0两种情况证明
的值;(3)由题意,即证:OA⊥OB,分y0≠0和y0=0两种情况证明![]() ,原题即得证.
,原题即得证.
(1)解:设F2,M的坐标分别为![]()
因为点M在双曲线C上,所以![]() ,即
,即![]() ,所以
,所以![]()
在Rt△MF2F1中,![]() ,
,![]() ,所以
,所以![]()
由双曲线的定义可知:![]()
故双曲线C的方程为:![]()
(2)解:由条件可知:两条渐近线分别为![]()
设双曲线C上的点P(x0,y0),设两渐近线的夹角为θ,则
则点P到两条渐近线的距离分别为
因为P(x0,y0)在双曲线C:![]() 上,所以
上,所以![]() ,又
,又![]() ,
,
所以![]() =
=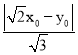
 cos(π-θ)=-
cos(π-θ)=-![]()
![]() =-
=-![]()
(3)证明:由题意,即证:OA⊥OB.
设A(x1,y1),B(x2,y2),切线l的方程为:x0x+y0y=2
①当y0≠0时,切线l的方程代入双曲线C中,化简得:![]()
所以: ,
,
又![]()
所以
②当y0=0时,易知上述结论也成立.所以![]()
综上,OA⊥OB,所以![]() .
.

 天天练口算系列答案
天天练口算系列答案【题目】某企业为提高生产质量,引入了一批新的生产设备,为了解生产情况,随机抽取了新、旧设备生产的共200件产品进行质量检测,统计得到产品的质量指标值如下表及图(所有产品质量指标值均位于区间![]() 内),若质量指标值大于30,则说明该产品质量高,否则说明该产品质量一般.
内),若质量指标值大于30,则说明该产品质量高,否则说明该产品质量一般.
质量指标 | 频数 |
| 2 |
| 8 |
| 10 |
| 30 |
| 20 |
| 10 |
合计 | 80 |

(1)根据上述图表完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为产品质量高与引人新设备有关;
的把握认为产品质量高与引人新设备有关;
新旧设备产品质量![]() 列联表
列联表
产品质量高 | 产品质量一般 | 合计 | |
新设备产品 | |||
旧设备产品 | |||
合计 |
(2)从旧设备生产的质量指标值位于区间![]() 的产品中,按分层抽样抽取6件产品,再从这6件产品中随机选取2件产品进行质量检测,求至少有一件产品质量指标值位于
的产品中,按分层抽样抽取6件产品,再从这6件产品中随机选取2件产品进行质量检测,求至少有一件产品质量指标值位于![]() 的概率.
的概率.
附: ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |



