题目内容
【题目】已知函数![]() .
.
(1)讨论f(x)的单调性;
(2)求函数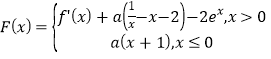 的零点个数.
的零点个数.
【答案】(1)见解析;(2)故a<0或a=e时,F(x)在y轴两侧各有1个零点,共2个零点,当a=0时,a(x+1)恒为0,F(x)有无数个零点.
【解析】
(1)对函数求导得到f′(x)=(x+1)(ex+a),分情况讨论导函数的正负,进而得到函数的单调性;(2)主要分析函数第一段的零点情况,令g(x)=xex﹣a(x>0),g′(x)=(x+1)ex>0,可得到函数g(x)单调增,通过讨论g(0)=﹣a和0的关系得到零点个数.
(1)f′(x)=(x+1)(ex+a),
a≥0时,x∈(﹣∞,﹣1)时,f′(x)<0,
x∈(﹣1,+∞)时,f′(x)>0,
故f(x)在(﹣∞,﹣1)递减,在(﹣1,+∞)递增,
a<0时,由f′(x)=0,解得:x=﹣1或x=ln(﹣a),
若a=﹣![]() ,则ln(﹣a)=﹣1,f′(x)≥0恒成立,
,则ln(﹣a)=﹣1,f′(x)≥0恒成立,
故f(x)在R递增,
若﹣![]() <a<0,则ln(﹣a)<﹣1,
<a<0,则ln(﹣a)<﹣1,
故x∈(﹣∞,ln(﹣a))∪(﹣1,+∞)时,f′(x)>0,
当x∈(ln(﹣a),﹣1)时,f′(x)<0,
故f(x)在(ln(﹣a),﹣1)递减,在(﹣∞,ln(﹣a)),(﹣1,+∞)递增;
若a<﹣![]() ,则ln(﹣a)>﹣1,
,则ln(﹣a)>﹣1,
当x∈(﹣∞,﹣1)∪(ln(﹣a),+∞)时,f′(x)>0,
当x∈(﹣1,ln(﹣a)时,f′(x)<0,
故f(x)在(﹣1,ln(﹣a))递减,在(﹣∞,﹣1),(ln(﹣a),+∞)递增,
综上,当a≥0时,f(x)在(﹣∞,﹣1)递减,在(﹣1,+∞)递增,
当﹣![]() <a<0时,f(x)在(ln(﹣a),﹣1)递减,在(﹣∞,ln(﹣a)),(﹣1,+∞)递增,
<a<0时,f(x)在(ln(﹣a),﹣1)递减,在(﹣∞,ln(﹣a)),(﹣1,+∞)递增,
当a=﹣![]() 时,f(x)在R递增,
时,f(x)在R递增,
当a<﹣![]() 时,f(x)在(﹣1,ln(﹣a))递减,在(﹣∞,﹣1),(ln(﹣a),+∞)递增;
时,f(x)在(﹣1,ln(﹣a))递减,在(﹣∞,﹣1),(ln(﹣a),+∞)递增;
(2)由已知得F(x)=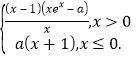 ,
,
令g(x)=xex﹣a(x>0),g′(x)=(x+1)ex>0,
故g(x)在(0,+∞)递增,
则g(x)>g(0)=﹣a,
故a<0或a=e时,F(x)在y轴两侧各有1个零点,共2个零点,
当a=0时,a(x+1)恒为0,F(x)有无数个零点.

【题目】《中华人民共和国民法总则》(以下简称《民法总则》)自2017年10月1日起施行.作为民法典的开篇之作,《民法总则》与每个人的一生息息相关.某地区为了调研本地区人们对该法律的了解情况,随机抽取50人,他们的年龄都在区间![]() 上,年龄的频率分布及了解《民法总则》的入数如下表:
上,年龄的频率分布及了解《民法总则》的入数如下表:
年龄 |
|
|
|
|
|
|
频数 | 5 | 5 | 10 | 15 | 5 | 10 |
了解《民法总则》 | 1 | 2 | 8 | 12 | 4 | 5 |
(1)填写下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为以45岁为分界点对了解《民法总则》政策有差异;
的把握认为以45岁为分界点对了解《民法总则》政策有差异;
年龄低于45岁的人数 | 年龄不低于45岁的人数 | 合计 | |
了解 |
|
| |
不了解 |
|
| |
合计 |
(2)若对年龄在![]() ,
,![]() 的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解《民法总则》的人数为
的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解《民法总则》的人数为![]() ,求随机变量的分布列和数学期望.
,求随机变量的分布列和数学期望.
参考公式和数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |