题目内容

【题目】《五曹算经》是我国南北朝时期数学家甄鸾为各级政府的行政人员编撰的一部实用算术书.其第四卷第九题如下：“今有平地聚粟，下周三丈高四尺，问粟几何？”其意思为“场院内有圆锥形稻谷堆，底面周长3丈，高4尺，那么这堆稻谷有多少斛？”已知1丈等于10尺，1斜稻谷的体积约为1.62立方尺，圆周率约为3，估算出堆放的稻谷约有（ ）

A.57.08斜B.171.24斛C.61.73斛D.185.19斛

【答案】C

【解析】

根据圆锥的周长求出底面半径，再计算圆锥的体积，从而估算堆放的稻谷数．

设圆锥形稻谷堆的底面半径为尺，

则底面周长为尺，解得尺，

又高为尺，

所以圆锥的体积为（立方尺）；

又（斛，

所以估算堆放的稻谷约有61.73（斛．

故选：．

练习册系列答案
相关题目

【题目】设、是两条不同的直线，、、是三个不同的平面，则的一个充分条件是（ ）

A.存在一条直线，，

B.存在一条直线，，

C.存在一个平面，满足，

D.存在两条异面直线，，，，，

【题目】已知函数．

（1）讨论f（x）的单调性；

（2）求函数的零点个数．

【题目】若函数y＝f(x)(x∈R)满足f(1+x)＝f(1-x)且x∈[－1，1]时，f(x)＝1－x2，函数g(x)＝则函数h(x)＝f(x)－g(x)在区间[－5，5]内的零点的个数为

A. 7 B. 8 C. 9 D. 10

【题目】设.

（1）讨论f(x)的单调性；

（2）当x>0时，f(x)>0恒成立，求k的取值范围.

【题目】某居民小区有两个相互独立的安全防范系统(简称系统)和，系统和在任意时刻发生故障的概率分别为和.

（1）求在任意时刻至少有一个系统不发生故障的概率；

（2）设系统在3次相互独立的检测中不发生故障的次数为随机变量，求的概率分布列及数学期望.(用数字作答)

【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，已知.

(1)求角C的值；

(2)若c＝2，且△ABC的面积为，求a，b.

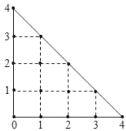
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形的顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收货量(单位：kg)与它的“相近”作物株数之间的关系如下表所示：

X

1

2

3

4

Y

51

48

45

42

这里，两株作物“相近”是指它们之间的直线距离不超过1米．

（Ⅰ）完成下表,并求所种作物的平均年收获量;

Y

51

48

45

42

频数


4



(Ⅱ)在所种作物中随机选取一株,求它的年收获量至少为48kg的概率.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网